【题目】在如图所示的平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=
x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB= ![]() PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;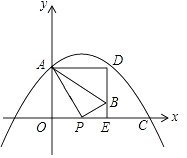
(1)求抛物线的解析式;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵抛物线y=﹣ ![]() x2+bx+c过点A(0,4)和C(8,0),
x2+bx+c过点A(0,4)和C(8,0),
∴ 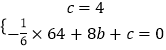 ,
,
解得 ![]() .
.
故所求的抛物线解析式为:y=﹣ ![]() x2+
x2+ ![]() x+4;
x+4;
(2)解:∵∠AOP=∠PEB=90°,∠OAP=∠EPB=90°﹣∠APO,
∴△AOP∽△PEB且相似比为 ![]() =
= ![]() =2,
=2,
∵AO=4,
∴PE=2,OE=OP+PE=t+2,
又∵DE=OA=4,
∴点D的坐标为(t+2,4),
∴点D落在抛物线上时,有﹣ ![]() (t+2)2+
(t+2)2+ ![]() (t+2)+4=4,
(t+2)+4=4,
解得t=3或t=﹣2,
∵t>0,
∴t=3.
故当t为3时,点D落在抛物线上;
(3)解:存在t,能够使得以A、B、D为顶点的三角形与△AOP相似,理由如下:
①当0<t<8时,如图1.
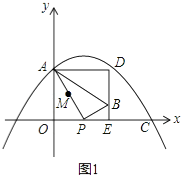
若△POA∽△ADB,则PO:AD=AO:BD,
即t:(t+2)=4:(4﹣ ![]() t),
t),
整理,得t2+16=0,
∴t无解;
若△POA∽△BDA,同理,解得t=﹣2±2 ![]() (负值舍去);
(负值舍去);
②当t>8时,如图2.
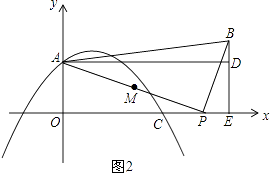
若△POA∽△ADB,则PO:AD=AO:BD,
即t:(t+2)=4:( ![]() t﹣4),
t﹣4),
解得t=8±4 ![]() (负值舍去);
(负值舍去);
若△POA∽△BDA,同理,解得t无解.
综上可知,当t=﹣2+2 ![]() 或8+4
或8+4 ![]() 时,以A、B、D为顶点的三角形与△AOP相似.
时,以A、B、D为顶点的三角形与△AOP相似.
【解析】先将A、C两点的坐标代入抛物线y=﹣ ![]() x2+bx+c,利用待定系数法求出b、c的值即可;(2)先判断出△AOP∽△PEB得出其相似比,进而求出D点的坐标,代入y=﹣
x2+bx+c,利用待定系数法求出b、c的值即可;(2)先判断出△AOP∽△PEB得出其相似比,进而求出D点的坐标,代入y=﹣ ![]() x2+
x2+ ![]() x+4即可求出t的值;(3)存在t,能够使得以A、B、D为顶点的三角形与△AOP相似,①当0<t<8时,若△POA∽△ADB,则PO:AD=AO:BD,从而t:(t+2)=4:(4﹣
x+4即可求出t的值;(3)存在t,能够使得以A、B、D为顶点的三角形与△AOP相似,①当0<t<8时,若△POA∽△ADB,则PO:AD=AO:BD,从而t:(t+2)=4:(4﹣ ![]() t)无解,若△POA∽△BDA,同理,解得t=﹣2±2
t)无解,若△POA∽△BDA,同理,解得t=﹣2±2 ![]() (负值舍去),②当t>8时若△POA∽△ADB,则PO:AD=AO:BD,即t:(t+2)=4:(
(负值舍去),②当t>8时若△POA∽△ADB,则PO:AD=AO:BD,即t:(t+2)=4:( ![]() t﹣4),解得t=8±4
t﹣4),解得t=8±4 ![]() (负值舍去),若△POA∽△BDA,同理,解得t无解.综上所述得出结论。
(负值舍去),若△POA∽△BDA,同理,解得t无解.综上所述得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价比乙种图书的单价多10元,且购买3本甲种图书和2本乙种图书共需花费130元
(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共50本,且投入总经费不超过1200元,则最多可以购买甲种图书多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=
 ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个图形中,既是中心对称图形又是轴对称图形的是( )
A.
B.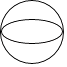
C.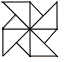
D.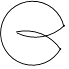
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用960元购进一批服装,并以每件46元的价格全部售完
 由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售. 该服装店第一次购买了此种服装多少件?
该服装店第一次购买了此种服装多少件? 两次出售服装共盈利多少元?
两次出售服装共盈利多少元?
相关试题

