【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.

(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°
参考答案:
【答案】(1)AD∥BC,见解析;(2)AB∥EF,见解析;(3)见解析.
【解析】
(1)欲证明AD∥BC,只要证明∠ADF=∠BCF即可;
(2)结论:AB∥EF,只要证明∠E=∠ABE 即可;
(3)只要证明∠OAB+∠OBA=90°即可解决问题;
解:(1)结论:AD∥BC.
理由如下:
∵∠ADE+∠ADF=180°,
∠ADE+∠BCF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)结论:AB与EF的位置关系是:AB∥EF.
理由:
∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC.
∠ABC.
又∵∠ABC=2∠E,
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠ABE.
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠OAB=![]() DAB,∠OBA=
DAB,∠OBA=![]() ∠CBA,
∠CBA,
∴∠OAB+∠OBA=90°,
∴∠EOF=∠AOB=90°,
∴∠E+∠F=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,求证EG=BE+GD.

(2)请用(1)的经验和知识完成此题:如图2,在四边形ABCD中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE.

(1)如图1,求证:AD∥BC
(2)若∠DAE和∠DCE的角平分线相交于点F.如图2,若∠BAE=80°,求∠F的度数
(3)如图3,∠DCE的角平分线的平分线交AE于点G,连接AC,若∠BAC=∠DAE,∠AGC=3∠CAE,则∠CAE的度数为________(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班要购买一批篮球和足球.已知篮球的单价比足球的单价贵40元,花1500元购买的篮球的个数与花900元购买的足球的个数恰好相等.
(1)篮球和足球的单价各是多少元?
(2)若该班恰好用完1000元购买的篮球和足球,则购买的方案有哪几种?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批排球和足球,已知购买2个排球和1个足球共需321元,购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价;
(2)若学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买足球多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,在
,在 上取一点
上取一点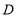 ,在
,在 延长线上取一点
延长线上取一点 ,且
,且 .证明:
.证明: .
.
(1)根据图1及证法一,填写相应的理由;
证法一:如图
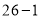 中,作
中,作 于
于 ,
, 交
交 的延长线于
的延长线于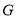 .
.
 ( )
( ) ,
,
 ( )
( ) ( )
( ) ,
, ,
, ( )
( ) ( )
( )(2)利用图2探究证法二,并写出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD的周长是32cm,∠ABC的平分线交AD所在直线于点E,且AE:ED=3:2,则AB的长为_____.
相关试题

