Question

【题目】（1）如图1，在正方形ABCD中，E是AB上一点，G是AD上一点，∠ECG=45°，求证EG=BE+GD．

（2）请用（1）的经验和知识完成此题：如图2，在四边形ABCD中，AG//BC(BC>AG)，∠B=90°，AB=BC=12，E是AB上一点，且∠ECG=45°，BE=4，求EG的长？

Answer 1

【答案】（1）证明见解析；（2）EG=10．

【解析】

（1）延长AD至F，使DF=BE，连接CF，根据正方形的性质，可直接证明△EBC≌△FDC，从而得出∠BCE=∠DCF，根据∠GCE=45°，得∠GCF=∠GCE=45°，利用全等三角形的判定方法得出△ECG≌△FCG，即GE=GF，即可证出EG=BE+GD；

（2）过C作CD⊥AG，交AG延长线于D，则四边形ABCD是正方形，设EG=x，则AE=8，根据（1）可得：AG=16-x，在直角△ADE中利用勾股定理即可求解．

（1）证明：如图3所示，延长AD至F，使DF=BE，连接CF，

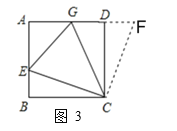
∵四边形ABCD是正方形，

∴BC=DC，∠ABC=∠ADC=∠BCD=90°，

∵∠CDF=180°-∠ADC，

∴∠CDF=90°，

∴∠ABC=∠CDF，

∵BE=DF，

∴△EBC≌△FDC，

∴∠BCE=∠DCF，EC=FC，

∵∠ECG=45°，

∴∠BCE+∠GCD=90°-∠ECG=90°-45°=45°，

∴∠GCD+∠DCF=∠FCG=45°，

∴∠ECG=∠FCG．

∵GC=GC，EC=FC，

∴△ECG≌△FCG，

∴EG=GF．

∵GF=GD+DF= BE+GD，

∴EG= BE+GD．

（2）解：如图4，过C作CD⊥AG，交AG延长线于D，

在直角梯形ABCD中，

∵AG∥BC，∠A=∠B=90°，

又∠CDA=90°，AB=BC，

∴四边形ABCD为正方形．

∴AD=AB=BC=12．

已知∠ECG=45°，根据（1）可知，EG=BE+DG，

设EG=x，则AG=AD-DG= AD-(EG-BE)=12-(x-4)=16-x，

∴AE=12-BE=12-4=8．

在Rt△AEG中

∵EG2=AG2+AE2，

即x2=（16-x）2+82，

解得：x=10．

∴EG=10．