【题目】如图,矩形OABC中,点A,C分别在x轴,y轴的正半轴上,OA=4,OC=2.点P(m,0)是射线OA上的动点,E为PC中点,作□OEAF,EF交OA于G,
(1)写出点E,F的坐标(用含m的代数式表示):E(_____,_____),F(______,_____).
(2)当线段EF取最小值时,m的值为______;此时□OEAF的周长为______.
(3)①当□OEAF是矩形时,求m的值.
②将△OEF沿EF翻折到△O′EF,若△O′EF与△AEF重叠部分的面积为1时,m的值为 .


参考答案:
【答案】(1)(![]() ,1),(4-
,1),(4-![]() ,-1);(2)4;4
,-1);(2)4;4![]() ;(3)①m=4±2
;(3)①m=4±2![]() ,②2或6.
,②2或6.
【解析】
(1)根据中点坐标公式和对称性,分别求出点E、F的坐标.
(2)由题意当EF⊥OA时,线段EF有最小值.由勾股定理可得m的值及四边形OEAF的周长.
(3)①分情况讨论:当点P在线段OA上时,如图1,利用勾股定理求出HG,就可得到OH的长,然后求出OP的长;当点P在OA延长线上时, 先求出OH,然后求出OP的长即可;②分两种情况:当点P在线段OA上时,先证△AEF为直角三角形,然后用勾股定理列方程求出m的值;当点P在OA延长线上时,先证△AFE为直角三角形,然后用勾股定理列方程求出m的值.
(1)∵C(0,2),P(m,0),由中点坐标公式,得点E的坐标为(![]() ,1),由F和E关于点G对称,可得F的坐标为(4-
,1),由F和E关于点G对称,可得F的坐标为(4-![]() ,-1).
,-1).
故答案为:(![]() ,1),(4-
,1),(4-![]() ,-1).
,-1).
(2)当EF⊥OA时,此时EG最小,则EF最小.此时点P与A重合,m=4,易知,四边形OEAF是菱形, 由勾股定理得OE=![]() ,四边形OEAF的周长为4
,四边形OEAF的周长为4![]() ,
,
故答案为:4,4![]()
(3)作EH⊥x轴于点H,
当点P在线段OA上时,如图1,
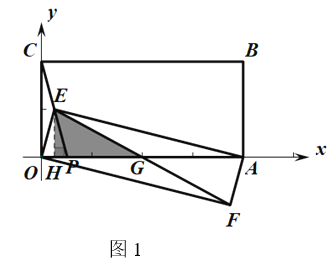
Rt△EHG中,EH=1,EG=OG=2,则HG= ![]()
∴OH=2- ![]()
∴m=OP=4-2 ![]()
当点P在OA延长线上时,如图2,
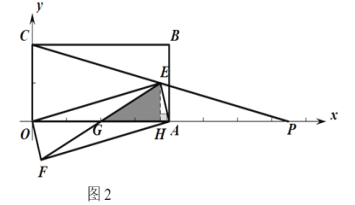
∴OH=2+ ![]()
∴m=OP=4+2 ![]()
综上所述,m=4 ±2 ![]()
②分两种情况:
Ⅰ:当P在线段OA上时,如图,
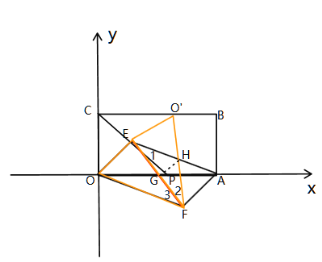
∵OEAF是平行四边形,
∴AG=![]() OA=2,
OA=2,
又E (![]() )
)
∴![]()
∵![]() 折叠后与
折叠后与![]() 重合
重合
∴![]()
又OF∥AE,
∴![]()
∴![]()
∴EH=FH
又G为EF中点
∴HG⊥EF
∵![]()
∴![]()
∴![]()
∴HE=AH
∴HE=AH=HF
∴△AEF为直角三角形,∠AFE=90°
∴∠OEG=90°
∴![]() +
+![]() =
=![]()
∴![]() +
+![]() +
+![]() +
+![]() =
=![]()
解得![]() =2
=2
Ⅱ、当P在OA的延长线上时,如图
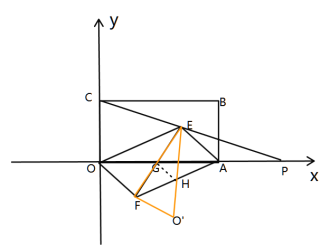
同理可证,EH=FH=AH,
∴∠AEF=90°
∴△AEG为直角三角形,
∴![]() +
+![]() =
=![]()
∴![]() +
+![]() +
+![]() +
+![]() =
=![]()
解得![]() =6
=6
综上所述,m=2或6
故答案为:m=2或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】华为手机新款上市,十分畅销.某经销商进价每台3000元,售价每台4000 元.一月份销量为512台,二、三月份销量持续走高,三月份销量达到800台.
(1)求二、三月份每月销量的平均增长率;
(2)根据市场调查经验,四月份此款手机销售情况将不再火爆而是趋于平稳.若售价不变,四月份销量将与三月份持平;若降价促销,每台每降价50元,月销量将增加100台.要使四月份利润达到90万元,每台应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将□ABCD的边DC延长至点E,使得CE=DC,连结AE,AC,BE,且AE交BC于点F.
(1)求证:AE与BC互相平分;
(2)若∠AFC=2∠D,AD=10.
①求证:四边形ABEC是矩形;
②连结FD,则线段FD的长度的取值范围为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 中,
中,  ,
,  ,
,  .
.

(
 )点
)点 从点
从点 开始沿
开始沿 边向
边向 以
以 的速度移动,点
的速度移动,点 从
从 点开始沿
点开始沿 边向点
边向点 以
以 的速度移动,如果
的速度移动,如果 ,
,  分别从
分别从 ,
,  同时出发,经过几秒,使
同时出发,经过几秒,使 的面积等于
的面积等于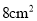 ?
?(
 )点
)点 从点
从点 开始沿
开始沿 边向
边向 以
以 的速度移动,点
的速度移动,点 从
从 点开始沿
点开始沿 边向点
边向点 以
以 的速度移动,如果
的速度移动,如果 ,
,  分别从
分别从 ,
,  同时出发,线段
同时出发,线段 能否将
能否将 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.(
 )若
)若 点沿射线
点沿射线 方向从
方向从 点出发以
点出发以 的速度移动,点
的速度移动,点 沿射线
沿射线 方向从
方向从 点出发以
点出发以 的速度移动,
的速度移动,  ,
,  同时出发,问几秒后,
同时出发,问几秒后,  的面积为
的面积为 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

-
科目: 来源: 题型:
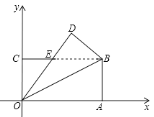
查看答案和解析>>【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
相关试题

