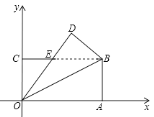
【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)见解析; (2)(3,4); (3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由矩形的性质得出OA∥BC,∠AOB=∠OBC,
由折叠的性质得∠AOB=∠DOB,得出∠OBC=∠DOB,证出OE=BE即可;
(2)设OE=BE=x,则CE=8-x,在Rt△OCE中,由勾股定理得出方程,解方程即可;
(3)先求出点D的坐标,然后根据B、D、E三点的坐标利用中点坐标公式分三种情况,即可求出P点的坐标.[点(a,b)与(c,d)所连线段的中点坐标是(![]() ,
,![]() )]
)]
解:
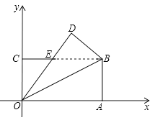
(1)证明:∵四边形OABC是矩形,
∴OA∥BC,
∴∠AOB=∠OBC,
由折叠的性质得:∠AOB=∠DOB,
∴∠OBC=∠DOB,
∴OE=BE,
∴△OBE是等腰三角形;
(2)设OE=BE=x,则CE=BC-BE=OA-BE=8-x,
在Rt△OCE中,由勾股定理得:42+(8-x)2=x2,
解得:x=5,
∴CE=8-x=3,
∵OC=4,
∴E点的坐标为(3,4);
(3)坐标平面内存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形。理由如下:
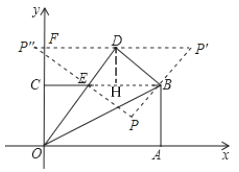
作DH⊥BE于H
在Rt△BDE中,BE=5,BD=4,DE=3
∴![]()
∴DH=![]()
∴EH=![]()
∴CH=![]()
∴点D的坐标是(![]() ,
,![]() )
)
∴当BE为平行四边形的对角线时,点P的坐标为(3+8-![]() ,4+4-
,4+4-![]() ),即(
),即(![]() ,
,![]() );
);
当BD为平行四边形的对角线时,点P的坐标为(8+![]() -3,4+
-3,4+![]() -4),即(
-4),即(![]() ,
,![]() );
);
当DE为平行四边形的对角线时,点P的坐标为(3+![]() -8,4+
-8,4+![]() -4),即(
-4),即(![]() ,
,![]() );
);
综上所述,坐标平面内存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形,P点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 中,
中,  ,
,  ,
,  .
.

(
 )点
)点 从点
从点 开始沿
开始沿 边向
边向 以
以 的速度移动,点
的速度移动,点 从
从 点开始沿
点开始沿 边向点
边向点 以
以 的速度移动,如果
的速度移动,如果 ,
,  分别从
分别从 ,
,  同时出发,经过几秒,使
同时出发,经过几秒,使 的面积等于
的面积等于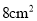 ?
?(
 )点
)点 从点
从点 开始沿
开始沿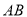 边向
边向 以
以 的速度移动,点
的速度移动,点 从
从 点开始沿
点开始沿 边向点
边向点 以
以 的速度移动,如果
的速度移动,如果 ,
,  分别从
分别从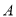 ,
,  同时出发,线段
同时出发,线段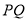 能否将
能否将 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.(
 )若
)若 点沿射线
点沿射线 方向从
方向从 点出发以
点出发以 的速度移动,点
的速度移动,点 沿射线
沿射线 方向从
方向从 点出发以
点出发以 的速度移动,
的速度移动,  ,
,  同时出发,问几秒后,
同时出发,问几秒后,  的面积为
的面积为 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC中,点A,C分别在x轴,y轴的正半轴上,OA=4,OC=2.点P(m,0)是射线OA上的动点,E为PC中点,作□OEAF,EF交OA于G,
(1)写出点E,F的坐标(用含m的代数式表示):E(_____,_____),F(______,_____).
(2)当线段EF取最小值时,m的值为______;此时□OEAF的周长为______.
(3)①当□OEAF是矩形时,求m的值.
②将△OEF沿EF翻折到△O′EF,若△O′EF与△AEF重叠部分的面积为1时,m的值为 .


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了决定谁将获得仅有的一张科普报告入场劵,甲和乙设计了如下的摸球游戏:在不透明的A、B两个口袋中分别放入编号分别为1,2,3的三个红球及一个白球,四个小球除了颜色和编号不同外,其他没有任何区别;甲在A口袋中摸出两个球,乙在B口袋中摸出一个球,如果甲摸出的两个球都是红色的甲得1分,否则,甲得0分,如果乙摸出的球是白色的,乙得1分,否则乙得0分,得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图的方法求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
相关试题

