【题目】根据要求回答问题:
(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.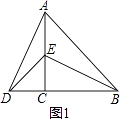
填空:线段AD,BE之间的关系为
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.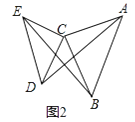
(3)解决问题
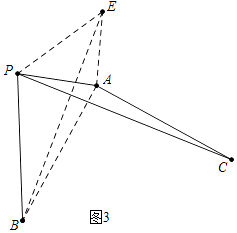
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.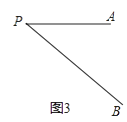
参考答案:
【答案】
(1)AD=BE,AD⊥BE
(2)解:结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.

∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
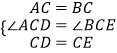 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)解:如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3﹣1中,当P、E、B共线时,BE最小,最小值=PB﹣PE=5﹣3 ![]() ,
,
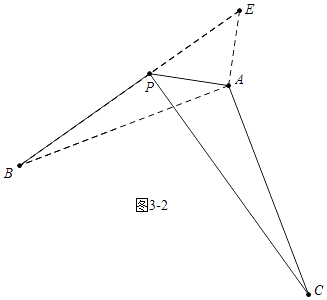
图3﹣2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3 ![]() ,
,
∴5﹣3 ![]() ≤BE≤5+3
≤BE≤5+3 ![]() ,
,
即5﹣3 ![]() ≤PC≤5+3
≤PC≤5+3 ![]() .
.

【解析】解:(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
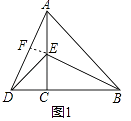
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
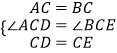 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
所以答案是AD=BE,AD⊥BE.
【考点精析】根据题目的已知条件,利用全等三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
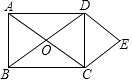
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有330台机器要运送到外地,计划租用甲、乙两种货车.已知甲种货车每辆租金400元,乙种货车每辆租金280元,若租用3辆甲种货车和2辆乙种货车,可运送195台机器;若租用4辆甲种货车和1辆乙种货车,可运送210台机器;
(1)求每辆甲种货车和乙种货车能运送的机器数量;
(2)请给出一次性将机器运送到目的地的最节省费用的租车方案,并说明理由. -
科目: 来源: 题型:
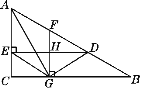
查看答案和解析>>【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判断四边形AEGF是否为菱形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】送报员李师傅骑摩托车从报社出发,先向西行驶3千米到达A村,继续向西行驶2千米到达B村,然后向东行驶10千米到达C村,最后回到报社.
(1)若把李师傅的出发地记为0(即以报社为原点),以向东方向为正方向,在数轴上表示出A、B、C三个村庄的位置;
(2)A、C两个村庄相距多远?
(3)送报员李师傅一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+5与坐标轴的交点B,C.已知D(0,3).
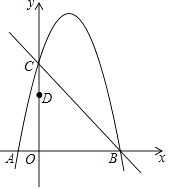
(1)求抛物线的解析式;
(2)M,N分别是BC,x轴上的动点,求△DMN周长最小时点M,N的坐标,并写出周长的最小值;
(3)连接BD,设M是平面上一点,将△BOD绕点M顺时针旋转90°后得到△B1O1D1 , 点B,O,D的对应点分别是B1 , O1 , D1 , 若△B1O1D1的两个顶点恰好落在抛物线上,请直接写出点O1的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一中学有学生3000名,2016年母亲节,晓彤为了调查本校大约有多少学生知道自己母亲的生日,随机调查了200名学生,有20名同学不知道自己母亲生日,关于这个数据收集和处理的问题,下列说法错误的是( )
A.个体是该校每一位学生
B.本校约有300名学生不知道自己母亲的生日
C.调查的方式是抽样调查
D.样本是随机调查的200名学生是否知道自己母亲的生日
相关试题

