【题目】如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是 . 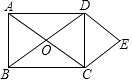
参考答案:
【答案】9
【解析】解:连接EO,延长EO交AB于H.
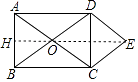
∵DE∥OC,CE∥OD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是矩形,
∴OD=OC,
∴四边形ODEC是菱形,
∴OE⊥CD,
∵AB∥CD,AD⊥CD,
∴EH⊥AB,AD∥OE,∵OA∥DE,
∴四边形ADEO是平行四边形,
∴AD=OE=6,
∵OH∥AD,OB=OD,
∴BH=AH,
∴OH= ![]() AD=3,
AD=3,
∴EH=OH+OE=3+6=9,
所以答案是9.
【考点精析】本题主要考查了三角形中位线定理和平行四边形的判定与性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
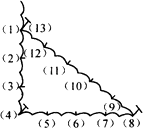
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.如果三角形两条边长的平方和等于第三边长的平方
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )
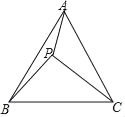
A.
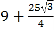 B.
B. 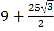 C.
C. 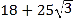 D.
D. 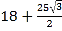
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有330台机器要运送到外地,计划租用甲、乙两种货车.已知甲种货车每辆租金400元,乙种货车每辆租金280元,若租用3辆甲种货车和2辆乙种货车,可运送195台机器;若租用4辆甲种货车和1辆乙种货车,可运送210台机器;
(1)求每辆甲种货车和乙种货车能运送的机器数量;
(2)请给出一次性将机器运送到目的地的最节省费用的租车方案,并说明理由. -
科目: 来源: 题型:
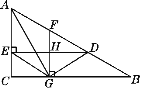
查看答案和解析>>【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判断四边形AEGF是否为菱形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求回答问题:
(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.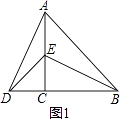
填空:线段AD,BE之间的关系为
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.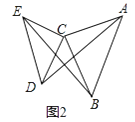
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.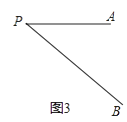
相关试题

