【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
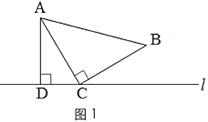
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
初步探究:
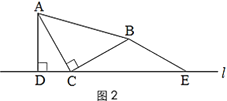
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
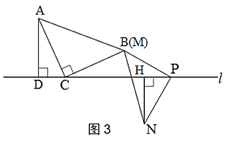
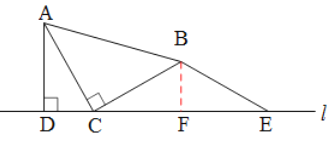
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
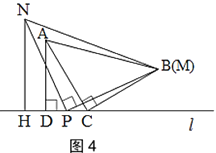
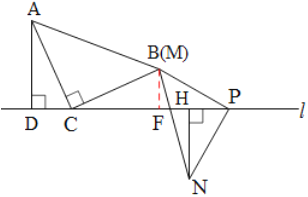
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
参考答案:
【答案】(1)CE=2AD;(2)A题:CP=AD+NH;B题:NH=![]() CD+AD.
CD+AD.
【解析】
(1) 过点B作BF⊥l于点F,通过已知条件证得△ACD≌△CBF,再通过等腰三角形性质即可求解.
(2) ①过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,即可得出边边之间关系.
②过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,再通过边边转化即可求解.
(1)CE=2AD,理由如下:
过点B作BF⊥l于点F,易得∠CFB=90°
∵AD⊥l
∴∠ADC=90°,∠CAD+∠DCA=90°
∴∠ADC=∠CFB
∵∠ACB=90°
∴∠DCA+∠BCF=90°
∴∠CAD=∠BCF
在△ACD和△CBF 中
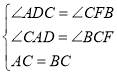
∴△ACD≌△CBF(AAS)
∴AD=CF
∵BE=BC,BF⊥l
∴CF=EF
∴CE=2CF=2AD
(2)A.CP=AD+NH,理由如下:
过点B作BF⊥l于点F,易得∠BFP=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP和△PHN 中

∴△BFP≌△PHN(AAS)
∴NH=PF
∵CP=CF+PF
∴CP=AD+NH
B.NH=![]() CD+AD,理由如下:
CD+AD,理由如下:
过点B作BF⊥l于点F,易得∠BFC=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP 和△PHN中

∴△BFP≌△PHN(AAS)
∴NH=PF
∵点P在线段CD的中点
∴CP=DP=![]() CD
CD
由图得:PF=PC+CF
∴NH=![]() CD+AD
CD+AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
-
科目: 来源: 题型:
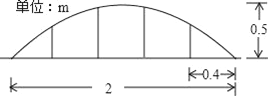
查看答案和解析>>【题目】某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某贸易公司购进“长青”胶州大白菜,进价为每棵20元,物价部门规定其销售单价每棵不得超过80元,也不得低于30元.经调查发现:日均销售量y(棵)与销售单价x(元/棵)满足一次函数关系,并且每棵售价60元时,日均销售90棵;每棵售价30元时,日均销售120棵.
(1)求日均销售量y与销售单价x的函数关系式;
(2)在销售过程中,每天还要支出其他费用200元,求销售利润w(元)与销售单价x之间的函数关系式;并求当销售单价为何值时,可获得最大的销售利润?最大销售利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 与函数
与函数 的图象交于
的图象交于 ,
,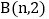 两点,
两点,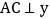 轴于C,
轴于C,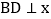 轴于D
轴于D 求k的值;
求k的值; 根据图象直接写出
根据图象直接写出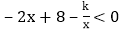 的x的取值范围;
的x的取值范围; 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若 和
和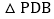 面积相等,求点P坐标.
面积相等,求点P坐标.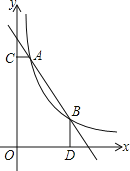
相关试题

