【题目】“低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)
(1)试写出z与x之间的函数关系式;
(2)请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?
(3)若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
参考答案:
【答案】
(1)解:依题意知,当销售单价定为x元时,年销售量减少 ![]() (x﹣100)万件,
(x﹣100)万件,
∴y=20﹣ ![]() (x﹣100)=﹣
(x﹣100)=﹣ ![]() x+30,
x+30,
即y与x之间的函数关系式是y=﹣ ![]() x+30.
x+30.
由题意得:
z=y(x﹣40)﹣2000
=(30﹣ ![]() x)(x﹣40)﹣2000
x)(x﹣40)﹣2000
=﹣ ![]() x2+34x﹣3200,
x2+34x﹣3200,
即z与x之间的函数关系是z=﹣ ![]() x2+34x﹣3200
x2+34x﹣3200
(2)解:∵z=﹣ ![]() x2+34x﹣3200,
x2+34x﹣3200,
=﹣ ![]() (x﹣170)2﹣310.
(x﹣170)2﹣310.
∴当x=170时,z取最大值,为﹣310,
即当销售单价为170元,年获利最大,并且第一年年底公司还差310万元就可收回全部投资.
(3)解:第二年的销售单价定为x元时,年获利为:
z=(30﹣ ![]() x)(x﹣40)﹣310=﹣
x)(x﹣40)﹣310=﹣ ![]() x2+34x﹣1510.
x2+34x﹣1510.
当z=1130时,即1130=﹣ ![]() x2+34x﹣1510,
x2+34x﹣1510,
整理得x2﹣340x+26400=0,
解得:x1=120,x2=220.
函数z=﹣ ![]() x2+34x﹣1510的图象大致如图所示,
x2+34x﹣1510的图象大致如图所示,
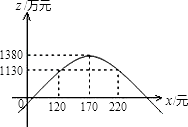
由图象可以看出:当120≤x≤220时,z≥1130.
故第二年的销售单价应确定在不低于120元且不高于220元的范围内.
【解析】(1)当销售单价定为x元时,依据题意可知年销售量减少![]() (x-100),从而可得到y与x之间的函数关系式,进而由题意易得z与x之间的函数关系;
(x-100),从而可得到y与x之间的函数关系式,进而由题意易得z与x之间的函数关系;
(2)利用配方法对z与x的函数关系进行变形,从而可得出当x=170时,z取最大值;即可得出公司是盈利了还是亏损;
(3)首先令获得的利润为1130万元列出方程,然后从而可求得此时x的值,然后依据函数的图形可确定出利润不低于1130万元时,自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度.
(1)当t=1时,d= ;
(2)当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;
(3)当点P运动到线段AB的3等分点时,直接写出d的值;
(4)当d=5时,直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生体育运动,某市第十七届中小学生田径运动会在市体育场举行,体育场主席台侧面如图所示,若顶棚顶端D与看台底端A的连线和地面垂直,测得顶棚CD的长为12米,∠BAC=30°,∠ACD=45°,求看台AC的长.(结果保留一位小数,参考数据:
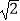 ≈1.41,
≈1.41, 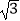 ≈1.73)
≈1.73)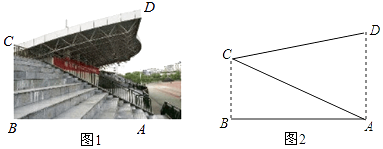
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
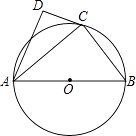
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
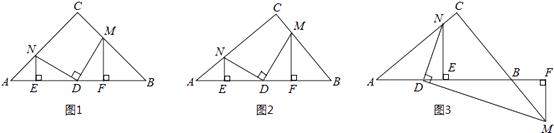
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
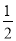 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:
①过一点有且只有一条直线与已知直线平行;
②若(t﹣4)2-3t=1,则t可以取的值有3个;
③多项式乘以单项式,积的次数等于多项式的次数与单项式次数的积
④关于x,y的方程组
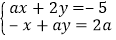 ,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当a每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是
,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当a每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是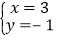 ,其中错误的是( )
,其中错误的是( )A. ②③④B. ①③④C. ②③D. ①②③
相关试题

