【题目】点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度.
(1)当t=1时,d= ;
(2)当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;
(3)当点P运动到线段AB的3等分点时,直接写出d的值;
(4)当d=5时,直接写出t的值.
![]()
参考答案:
【答案】(1)d=3;(2)d的值为3或![]() ;(3)所求d的值为0或4;(4)所求t的值为
;(3)所求d的值为0或4;(4)所求t的值为![]() 或5.
或5.
【解析】
(1)当t=1时,求出AP=1,BQ=2,根据PQ=AB﹣AP﹣BQ即可求解;
(2)分①P点恰好运动到线段AB的中点;②Q点恰好运动到线段AB的中点两种情况进行讨论;
(3)当点P运动到线段AB的3等分点时,分①AP=![]() AB;②AP=
AB;②AP=![]() AB两种情况进行讨论;
AB两种情况进行讨论;
(4)当d=5时,分①P与Q相遇之前;②P与Q相遇之后两种情况进行讨论.
(1)当t=1时,AP=1,BQ=2,
∵AB=4﹣(﹣2)=6,
∴PQ=AB﹣AP﹣BQ=3,即d=3.
故答案为3;
(2)线段AB的中点表示的数是:![]() =1.
=1.
①如果P点恰好运动到线段AB的中点,那么AP=![]() AB=3,t=
AB=3,t=![]() =3,
=3,
BQ=2×3=6,即Q运动到A点,
此时d=PQ=PA=3;
②如果Q点恰好运动到线段AB的中点,那么BQ=![]() AB=3,t=
AB=3,t=![]() ,
,
AP=1×![]() =
=![]() ,
,
则d=PQ=AB﹣AP﹣BQ=6﹣![]() ﹣3=
﹣3=![]() .
.
故d的值为3或![]() ;
;
(3)当点P运动到线段AB的3等分点时,分两种情况:
①如果AP=![]() AB=2,那么t=
AB=2,那么t=![]() =2,
=2,
此时BQ=2×2=4,P、Q重合于原点,
则d=PQ=0;
②如果AP=![]() AB=4,那么t=
AB=4,那么t=![]() =4,
=4,
∵动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动,
∴此时BQ=6,即Q运动到A点,
∴d=PQ=AP=4.
故所求d的值为0或4;
(4)当d=5时,分两种情况:
①P与Q相遇之前,
∵PQ=AB﹣AP﹣BQ,
∴6﹣t﹣2t=5,
解得t=![]() ;
;
②P与Q相遇之后,
∵P点运动到线段AB的中点时,t=3,此时Q运动到A点,停止运动,
∴d=AP=t=5.
故所求t的值为![]() 或5.
或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为
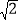 ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )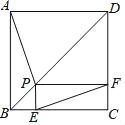
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线
 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.

请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生体育运动,某市第十七届中小学生田径运动会在市体育场举行,体育场主席台侧面如图所示,若顶棚顶端D与看台底端A的连线和地面垂直,测得顶棚CD的长为12米,∠BAC=30°,∠ACD=45°,求看台AC的长.(结果保留一位小数,参考数据:
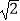 ≈1.41,
≈1.41, 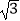 ≈1.73)
≈1.73)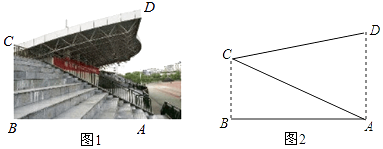
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
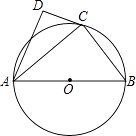
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)
(1)试写出z与x之间的函数关系式;
(2)请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?
(3)若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
相关试题

