【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC. 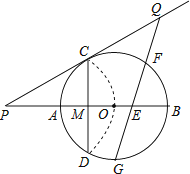
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
参考答案:
【答案】
(1)
解:如图,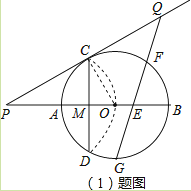
连接OC,
∵ ![]() 沿CD翻折后,点A与圆心O重合,
沿CD翻折后,点A与圆心O重合,
∴OM= ![]() OA=
OA= ![]() ×2=1,CD⊥OA,
×2=1,CD⊥OA,
∵OC=2,
∴CD=2CM=2 ![]() =2
=2 ![]() =2
=2 ![]() .
.
(2)
证明:∵PA=OA=2,AM=OM=1,CM= ![]() CD=
CD= ![]() ,∠CMP=∠OMC=90°,
,∠CMP=∠OMC=90°,
∴PC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵OC=2,PO=2+2=4,
∴PC2+OC2=(2 ![]() )2+22=16=PO2,
)2+22=16=PO2,
∴∠PCO=90°,
∴PC是⊙O的切线.
(3)
解:GEGF是定值,证明如下:如图 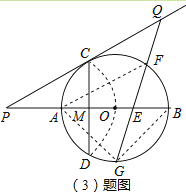 ,
,
连接GA、AF、GB,
∵点G为 ![]() 的中点,∴
的中点,∴ ![]() =
= ![]() ,
,
∴∠BAG=∠AFG,
又∵∠AGE=∠FGA,
∴△AGE∽△FGA,
∴ ![]() =
= ![]() ,
,
∴GEGF=AG2,
∵AB为直径,AB=4,
∴∠BAG=∠ABG=45°,
∴AG=2 ![]() ,
,
∴GEGF=8.
【解析】(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;
(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;
(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得 ![]() =
= ![]() ,从而得到GEGF=AG2 , 再根据等腰直角三角形的性质求解即可. 本题是圆的综合题型,主要利用了翻折变换的性质,垂径定理,勾股定理,勾股定理逆定理,圆的切线的定义,相似三角形的判定与性质,难点在于(3)作辅助线构造出相似三角形.
,从而得到GEGF=AG2 , 再根据等腰直角三角形的性质求解即可. 本题是圆的综合题型,主要利用了翻折变换的性质,垂径定理,勾股定理,勾股定理逆定理,圆的切线的定义,相似三角形的判定与性质,难点在于(3)作辅助线构造出相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)
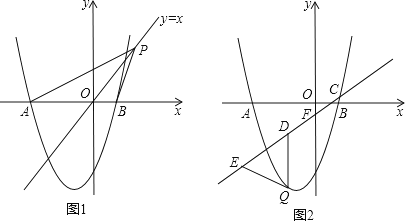
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y= x﹣
x﹣  分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧
 的中点,∠ABC=52°,则∠DAB等于( )
的中点,∠ABC=52°,则∠DAB等于( ) 
A.58°
B.61°
C.72°
D.64° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,下列给出四个结论中,正确结论的个数是( )个
①c>0;
②若点B(﹣ ,y1)、C(﹣
,y1)、C(﹣  ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ <0;
<0;
⑤4a﹣2b+c>0.
A.2
B.3
C.4
D.5
相关试题

