【题目】
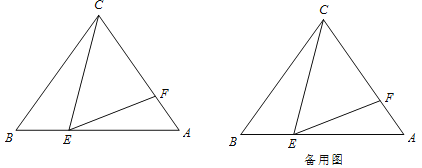
如图,在![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点(不与端点重合),点
上的动点(不与端点重合),点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,若在点
,若在点![]() 、点
、点![]() 的运动过程中,始终保证
的运动过程中,始终保证![]() 。
。
(1)求证:![]() ;
;
(2)当以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切时,求
相切时,求![]() 的长;
的长;
(3)探究:在点![]() 、点
、点![]() 的运动过程中,
的运动过程中,![]() 可能为等腰三角形吗?若能,求出
可能为等腰三角形吗?若能,求出![]() 的长;若不能,请说明理由。
的长;若不能,请说明理由。
参考答案:
【答案】(1)证明见解析;(2)BE的长为1或5;(3)当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.
【解析】试题分析(1)由∠B +∠B CE=∠CEA=∠CEF+∠FEA,∠CEF=∠B即可得∠AEF=∠BCE;(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA(如图),根据等腰三角形的性质可得BM=AM==3,在Rt△AMC中,根据勾股定理可得CF =CM=4,即可得AF=1,再证得△AEF∽△BCE,设设BE长为x,则EA长为6-x,根据相似三角形的性质列出方程求解即可;(3)分CE=CF,CF=EF,CF=EF三种情况求解即可.
试题解析:
(1)证明:∵∠B +∠B CE=∠CEA =∠CEF+∠FEA
∠CEF=∠B
∴∠AEF=∠BCE
(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA
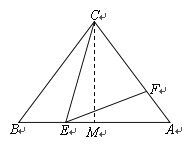
∵CA=CB,CM⊥BA ∴BM=AM=![]() =3
=3
Rt△AMC中,AC=5,AM=3,
∴CF =CM=4 ∴AF=1
∵ CA=CB ∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE
∴![]()
设BE长为x,则EA长为6-x
∴![]()
解得:x1=1,x2=5
答:BE的长为1或5.
(3)可能.

①当CE=CF时,∠3=∠2=∠A
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CF=EF时,
又∵△AEF∽△BCE
∴△AEF≌△BCE
∴AE=BC=5
∴BE=AB-5=1
③当CF=EF时,∠1=∠2=∠A=∠B
△FCE∽△CBA
∴![]()

∴![]()
∵△AEF∽△BCE
∴![]()
∴![]()
∴![]()
答:当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
,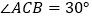 ,将
,将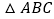 绕点
绕点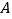 顺时针旋转得到
顺时针旋转得到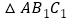 ,当点
,当点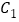 、
、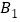 、
、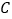 三点共线时,旋转角为
三点共线时,旋转角为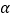 ,连接
,连接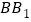 ,交
,交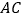 于点
于点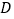 。下面结论:①
。下面结论:①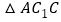 为等腰三角形;②
为等腰三角形;②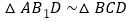 ;③
;③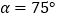 ;④
;④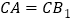 中,正确的是( )
中,正确的是( )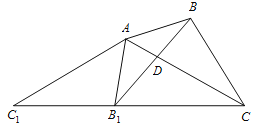
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组
(1)2x﹣3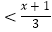
(2)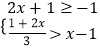 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
如图1,抛物线
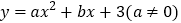 与x轴交于点
与x轴交于点 、点
、点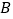 (点
(点 在点
在点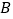 左侧),与
左侧),与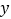 轴交于点
轴交于点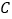 ,点
,点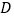 为顶点,已知点
为顶点,已知点 、点
、点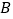 的坐标分别为
的坐标分别为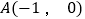 、
、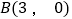 。
。(1)求抛物线的解析式;
(2)在直线
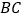 上方的抛物线上找一点
上方的抛物线上找一点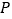 ,使
,使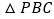 的面积最大,求
的面积最大,求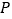 点坐标;
点坐标;(3)如图2,连结
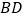 、
、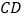 ,抛物线的对称轴与x轴交于点
,抛物线的对称轴与x轴交于点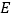 。过抛物线上一点
。过抛物线上一点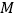 作
作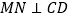 ,交直线
,交直线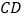 于点
于点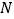 ,求当
,求当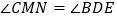 时点
时点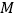 的坐标。
的坐标。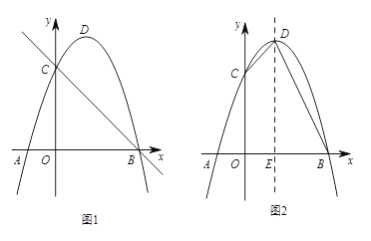
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为△ABC的三边,且a2c2﹣b2c2=a4﹣b4,则此三角形的形状为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子变形是因式分解的是【 】
A.x2-5x+6=x(x-5)+6 B.x2-5x+6=(x-2)(x-3)
C.(x-2)(x-3)=x2-5x+6 D.x2-5x+6=(x+2)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,4)到原点的距离是( )
A. 3 B. 4 C. 5 D. ±5
相关试题

