【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,则图中共有等腰三角形( )
,则图中共有等腰三角形( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
参考答案:
【答案】D
【解析】
根据等腰三角形性质和三角形内角和定理求出∠ACB=∠B=![]() (180°∠A)=72°,求出∠ACD=∠BCD=
(180°∠A)=72°,求出∠ACD=∠BCD=![]() ∠ACB=36°,求出∠CDB=∠A+∠ACD=72°,根据平行线的性质得出∠EDB=∠A=36°,∠DEB=∠ACB=72°,∠CDE=∠ACD=36°,推出∠A=∠ACD=∠BCD=∠CDE=36°,∠B=∠ACD=∠DEB=∠CDB=72°即可.
∠ACB=36°,求出∠CDB=∠A+∠ACD=72°,根据平行线的性质得出∠EDB=∠A=36°,∠DEB=∠ACB=72°,∠CDE=∠ACD=36°,推出∠A=∠ACD=∠BCD=∠CDE=36°,∠B=∠ACD=∠DEB=∠CDB=72°即可.
∵AB=AC,
∴∠ACB=∠B,
∵∠A=36°,
∴∠ACB=∠B=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=![]() ∠ACB=36°,
∠ACB=36°,
∴∠CDB=∠A+∠ACD=72°,
∵DE∥AC,
∴∠EDB=∠A=36°,∠DEB=∠ACB=72°,∠CDE=∠ACD=36°,
∴∠A=∠ACD=∠BCD=∠CDE=36°,∠B=∠ACD=∠DEB=∠CDB=72°,
∴△ACB、△ACD、△CDB、△CDE、△DEB都是等腰三角形,共5个,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(3x+5)2﹣(x﹣9)2=0;
(2)3x2﹣4x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程kx2﹣4x+2=0有实数根.
(1)求k的取值范围;
(2)若△ABC中,AB=AC=2,AB,BC的长是方程kx2﹣4x+2=0的两根,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
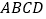 中,
中,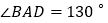 ,
,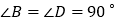 ,在
,在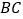 、
、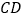 上分别找一点
上分别找一点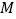 、
、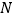 ,使三角形
,使三角形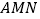 周长最小时,则
周长最小时,则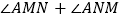 的度数为( )
的度数为( )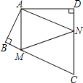
A.
 B.
B.  C.
C. 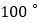 D.
D. 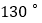
-
科目: 来源: 题型:
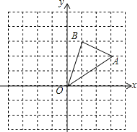
查看答案和解析>>【题目】如图,在边长为
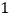 的正方形组成的网格中,
的正方形组成的网格中, 的顶点均在格点上,点
的顶点均在格点上,点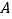 、
、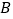 的坐标分别是
的坐标分别是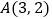 ,
,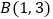 ,
, 关于
关于 轴对称的图形为
轴对称的图形为 .
.
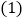 画出
画出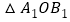 并写出点
并写出点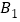 的坐标为________;
的坐标为________;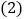 写出
写出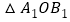 的面积为________;
的面积为________; 点
点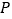 在
在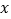 轴上,使
轴上,使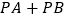 的值最小,写出点
的值最小,写出点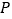 的坐标为________.
的坐标为________. -
科目: 来源: 题型:
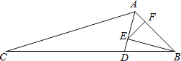
查看答案和解析>>【题目】如图,在
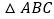 中,
中,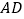 为
为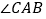 平分线,
平分线,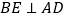 于
于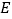 ,
,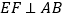 于
于 ,
,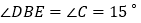 ,
,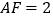 ,则
,则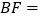 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 是等边三角形,
是等边三角形, ,
,
 请你判断
请你判断 的形状并说明理由;
的形状并说明理由; 如果
如果 绕点
绕点 旋转,交边
旋转,交边 于点
于点 ,请你判断
,请你判断 的周长是否发生变化?如果不变,说明理由;如果变化,说明当点
的周长是否发生变化?如果不变,说明理由;如果变化,说明当点 在什么位置时,
在什么位置时, 的周长最小.
的周长最小.
相关试题

