【题目】已知关于x的一元二次方程kx2﹣4x+2=0有实数根.
(1)求k的取值范围;
(2)若△ABC中,AB=AC=2,AB,BC的长是方程kx2﹣4x+2=0的两根,求BC的长.
参考答案:
【答案】
(1)解:∵方程有实数根,
∴△=b2﹣4ac=(﹣4)2﹣4×k×2=16﹣8k≥0,
解得:k≤2,
又因为k是二次项系数,所以k≠0,
所以k的取值范围是k≤2且k≠0
(2)解:由于AB=2是方程kx2﹣4x+2=0,
所以把x=2代入方程,可得k= ![]() ,
,
所以原方程是:3x2﹣8x+4=0,
解得:x1=2,x2= ![]() ,
,
所以BC的值是 ![]()
【解析】(1)若一元二次方程有实数根,则根的判别式△=b2﹣4ac≥0,建立关于k的不等式,即可求出k的取值范围.(2)由于AB=2是方程kx2﹣4x+2=0,所以可以确定k的值,进而再解方程求出BC的值.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对三角形三边关系的理解,了解三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.
-
科目: 来源: 题型:
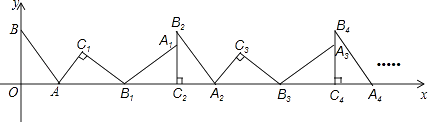
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B100的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(3x+5)2﹣(x﹣9)2=0;
(2)3x2﹣4x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 中,
中,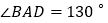 ,
,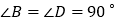 ,在
,在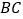 、
、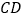 上分别找一点
上分别找一点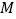 、
、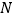 ,使三角形
,使三角形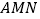 周长最小时,则
周长最小时,则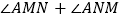 的度数为( )
的度数为( )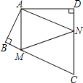
A.
 B.
B.  C.
C. 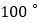 D.
D. 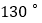
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,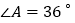 ,
, ,
, 平分
平分 ,
, ,则图中共有等腰三角形( )
,则图中共有等腰三角形( )
A.
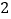 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
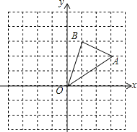
查看答案和解析>>【题目】如图,在边长为
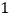 的正方形组成的网格中,
的正方形组成的网格中, 的顶点均在格点上,点
的顶点均在格点上,点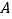 、
、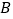 的坐标分别是
的坐标分别是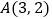 ,
,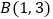 ,
, 关于
关于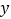 轴对称的图形为
轴对称的图形为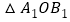 .
.
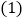 画出
画出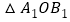 并写出点
并写出点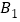 的坐标为________;
的坐标为________;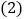 写出
写出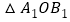 的面积为________;
的面积为________;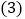 点
点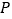 在
在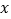 轴上,使
轴上,使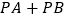 的值最小,写出点
的值最小,写出点 的坐标为________.
的坐标为________.
相关试题

