【题目】一自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产记为负
(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产自行车多少辆?
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超出部分每辆另加15元,少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
参考答案:
【答案】(1)213;(2)1409;(3)26;(4)85215;
【解析】
(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得答案;
(3)根据有理数的加法,可得答案;
(4)根据基本工资加奖金,可得答案.
(1)超产记为正、减产记为负,所以星期四生产自行车200+13辆,故该厂星期四生产自行车213辆;
(2) 根据题意524+1310+169=9,200×7+9=1409辆,
故该厂本周实际生产自行车1409辆;
(3)根据图示产量最多的一天是216辆,产量最少的一天是190辆,216190=26辆,
故产量最多的一天比产量最少的一天多生产自行车26辆;
(4)根据图示本周工人工资总额=(7×200+9)×60+9×15=85215元,
故该厂工人这一周的工资总额是85215元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个边长均为4的正方形重叠在一起,O1,O2是其中左侧两个正方形的对角线交点,同时O1,O2也是右侧两个正方形的顶点,根据教材第63页《实践与探究》活动中有关内容,可知阴影部分面积是( )

A.2B.4C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
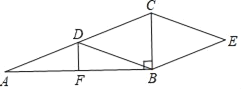
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边得中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是 .
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ,请证明你的猜想.
(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司有三个住宅区,A,B,C各区分别住有职工10人,15人,45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=150m,BC=90m.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点AB. 点BC. 点A,B之间D. 点C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

相关试题

