搜索
【题目】已知如图等腰
，
，
，
于点
.点
是
延长线上一点，
点是线段
上一点，
，下面的结论：①
平分
；②
；③
是等边三角形；④
.其中正确的序号是________.
参考答案：
【答案】①③④
【解析】
①利用等边对等角，即可证得；
②因为点O是线段AD上一点，所以BO不一定是
的角平分线，可作判断；
③证明
且OP=OC，即可证得
是等边三角形；
④首先证明
,则AO=CE，AC=AE+CE=AO+AP；
∵
，
，
∴AD平分
∴
∴
平分
①正确；
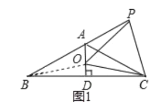
如图1，连接BO，∵AD垂直平分BC
∴OB=OC 又∵OC=OP
∴OB=OC=OP
∴
∵点O在线段AD上，∴
与
不一定相等，
则
与
不一定相等，故②不正确；
∵
∴
∵
∴
∴
又∵OP=OC
∴是等边三角形，故③正确；
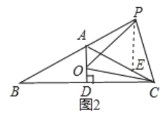
如图2，在AC上截取AE=PA，连接PB，
∵
∴
是等边三角形
∴
∴
∵
∴
∵OP=CP
∴
∴AO=CE
∴AC=AE+CE=AO+AP,故④正确；
本题正确的结论有：①③④
故答案为：①③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，点C在∠MON的一边OM上，过点C的直线AB∥ON，CD平分∠ACM，CE⊥CD．
（1）若∠O=50°，求∠BCD的度数；
（2）求证：CE平分∠OCA；
（3）当∠O为多少度时，CA分∠OCD成1：2两部分，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）
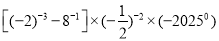；（2）
；（3）2x 5y3x 2 y 2x x 3y；
（4）（x+1）2（x-1）2（x2+1）2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知（x3+mx+n）（x2﹣3x+4）展开式中不含 x3和 x2项．
（1）求m、n的值；
（2）当 m、n取第（1）小题的值时，求（m+n）（m2﹣mn+n2）的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请把下列证明过程补充完整.已知:如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，∠1=∠2=∠E，∠3=∠4.求证:AB∥CD.
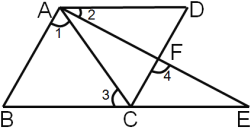
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ，即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解市民对“垃圾分类知识”的知晓程度。某数学学习兴趣小组对市民进行随机抽样的问卷调查。调查结果分为“A.非常了解”“B.了解”"C.基本了解”，“D不太了解”四个等级进行统计，并将统计结果检制成如下两幅不完整的统计图(图1，图2).请根据图中的信息解答下列问题。
(1)这次调查的市民人数为____ 人，图2中，
____(2)补全图1中的条形统计图；
(3)在图2中的扇形统计图中，求“C.基本了解”所在扇形的圆心角度数；
(4)据统计，2019年该市约有市民800万人，那么根据抽样调查的结果，可估计对“垃圾分类知识”的知晓程度为“D.不太了解”的市民约有多少万人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某慈善组织租用甲、乙两种货车共
辆，把蔬菜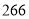
吨，水果
吨，全部运到灾区已知辆甲种货车同时可装蔬菜
吨，水果
吨；一辆乙种货车同时可装蔬菜吨，水果
吨.(1)若将这批货物一次性运到灾区，请写出具体的租车方案？
(2)若甲种货车每辆需付燃油费
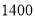元，乙种货车每辆需付燃油费
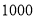元，则应选(1)种的哪种方案，才能使所付的燃油费最少？最少的燃油费是多少元？
相关试题
