【题目】某慈善组织租用甲、乙两种货车共![]() 辆,把蔬菜
辆,把蔬菜![]() 吨,水果
吨,水果![]() 吨,全部运到灾区已知辆甲种货车同时可装蔬菜
吨,全部运到灾区已知辆甲种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨;一辆乙种货车同时可装蔬菜
吨;一辆乙种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨.
吨.
(1)若将这批货物一次性运到灾区,请写出具体的租车方案?
(2)若甲种货车每辆需付燃油费![]() 元,乙种货车每辆需付燃油费
元,乙种货车每辆需付燃油费![]() 元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
参考答案:
【答案】(1)有3种租车方案:方案一:租甲种货车5辆,乙种货车11辆;
方案二:租甲种货车6辆,乙种货车10辆;方案三:租甲种货车7辆,乙种货车9辆;
(2)选择(1)中方案一租车,才能使所付的燃油费最少,最少燃油费为18000元.
【解析】
(1)设设租用甲种货车x辆,则租用乙种货车(16-x)辆,然后根据装运的蔬菜和水果数不少于所需要运送的吨数列出一元一次不等式组,求解后再根据x是正整数涉及租车方案;
(2)根据所付的燃油费等于两种车辆的燃油费之和列式整理,再根据一次函数的增减性求出费用的最小值.
(1)设租用甲种货车x辆,则租用乙种货车(16-x)辆,
根据题意得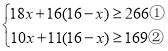
由①得![]()
由②得![]()
∴![]()
∵x为正整数
∴x=5或6或7
因此,有3种租车方案:
方案一:租甲种货车5辆,乙种货车11辆;
方案二:租甲种货车6辆,乙种货车10辆;
方案三:租甲种货车7辆,乙种货车9辆;
(2)由(1)知,租用甲种货车x辆,租用乙种货车(16-x)辆
设两种货车燃油总费用为y元
由题意得:![]()
![]()
∵![]()
∴y随x的增大而增大,当x=5时,y有最小值
∴y最小=![]() 元
元
答:选择(1)中方案一租车,才能使所付的燃油费最少,最少燃油费为18000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图等腰
 ,
,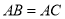 ,
, ,
, 于点
于点 .点
.点 是
是 延长线上一点,
延长线上一点, 点是线段
点是线段 上一点,
上一点, ,下面的结论:①
,下面的结论:① 平分
平分 ;②
;② ;③
;③ 是等边三角形;④
是等边三角形;④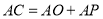 .其中正确的序号是________.
.其中正确的序号是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把下列证明过程补充完整.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
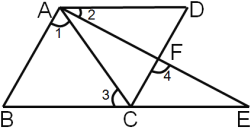
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ,即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解市民对“垃圾分类知识”的知晓程度。某数学学习兴趣小组对市民进行随机抽样的问卷调查。调查结果分为“A.非常了解”“B.了解”"C.基本了解”,“D不太了解”四个等级进行统计,并将统计结果检制成如下两幅不完整的统计图(图1,图2).请根据图中的信息解答下列问题。

(1)这次调查的市民人数为____ 人,图2中,
 ____
____(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“C.基本了解”所在扇形的圆心角度数;
(4)据统计,2019年该市约有市民800万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“D.不太了解”的市民约有多少万人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


相关试题

