【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
参考答案:
【答案】(1)-1,3;(2)-1<x<3;(3) 二次函数的解析式为y=-![]() x2+x+
x2+x+![]() .
.
【解析】
(1)根据抛物线解析式,求出对称轴,根据点A、B关于对称轴对称,求出点B的坐标即可;
(2)根据抛物线的开口方向,与x轴的交点,即可判定不等式的解集;
(3)根据抛物线经过点A,将其代入,用含a的式子表示出c,求出抛物线的顶点坐标,将其代入直线解析式,即可求出a的值,进而求出c的值即可.
(1)根据题意可知,抛物线的对称轴是:直线x=![]() .
.
∵点A(﹣1,0),∴点B的坐标为(3,0),∴一元二次方程的解为:﹣1,3;
故答案为:﹣1,3;
(2)∵二次函数与y轴正半轴交于点C,∴抛物线的开口向下,∴当ax2﹣2ax+c>0时,不等式的解集为:﹣1<x<3;
故答案为:﹣1<x<3;
(3)∵抛物线经过点A(﹣1,0),∴a+2a+c=0,即:c=﹣3a,∴﹣![]() =﹣3a﹣a=﹣4a.
=﹣3a﹣a=﹣4a.
∵抛物线的顶点坐标(1,﹣4a)在直线y=2x上,∴﹣4a=2×1,解得:a=﹣![]() ,∴c=﹣3a=3×
,∴c=﹣3a=3×![]() =
=![]() ,∴二次函数的解析式为:y=﹣
,∴二次函数的解析式为:y=﹣![]() x2+x+
x2+x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
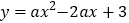 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与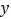 轴的交点为
轴的交点为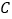 ,顶点为
,顶点为 .
.(1)求该二次函数的解析式及点
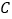 ,
, 的坐标;
的坐标;(2)点
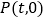 是
是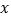 轴上的动点,
轴上的动点,①求
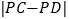 的最大值及对应的点
的最大值及对应的点 的坐标;
的坐标;②设
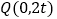 是
是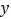 轴上的动点,若线段
轴上的动点,若线段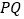 与函数
与函数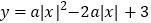 的图像只有一个公共点,求
的图像只有一个公共点,求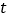 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
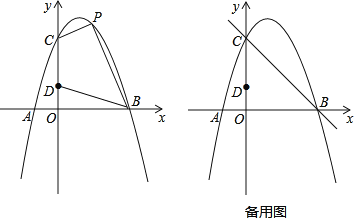
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
-
科目: 来源: 题型:
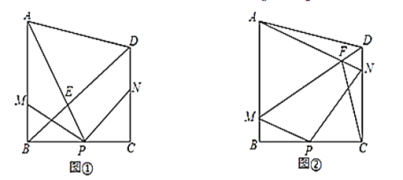
查看答案和解析>>【题目】如图,在四边形
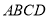 中,
中,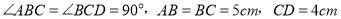 点
点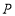 从点
从点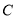 出发以
出发以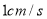 的速度沿
的速度沿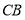 向点
向点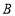 匀速移动,点
匀速移动,点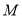 从点
从点 出发以
出发以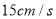 的速度沿
的速度沿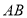 向点
向点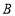 匀速移动,点
匀速移动,点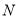 从点
从点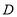 出发以
出发以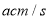 的速度沿
的速度沿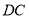 向点
向点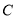 匀速移动.点
匀速移动.点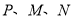 同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为
同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为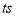 .
.(1)如图①,
①当
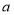 为何值时,点
为何值时,点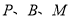 为顶点的三角形与
为顶点的三角形与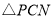 全等?并求出相应的
全等?并求出相应的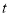 的值;
的值;②连接
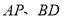 交于点
交于点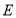 ,当
,当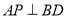 时,求出
时,求出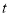 的值;
的值;(2)如图②,连接
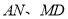 交于点
交于点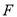 .当
.当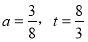 时,证明:
时,证明: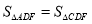 .
.
相关试题

