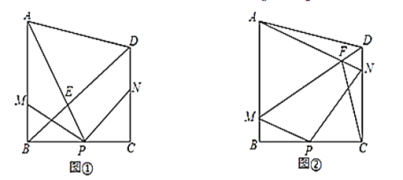
【题目】如图,在四边形![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,点
匀速移动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.点
匀速移动.点![]() 同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为
同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为![]() .
.
(1)如图①,
①当![]() 为何值时,点
为何值时,点![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?并求出相应的
全等?并求出相应的![]() 的值;
的值;
②连接![]() 交于点
交于点![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
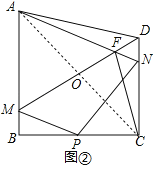
(2)如图②,连接![]() 交于点
交于点![]() .当
.当![]() 时,证明:
时,证明:![]() .
.
参考答案:
【答案】(1)①![]() ,
,![]() 或
或![]() ,
,![]() ;②
;②![]() ;(2)见解析
;(2)见解析
【解析】
(1)①当![]() 时或当
时或当![]() 时,分别列出方程即可解决问题;
时,分别列出方程即可解决问题;
②当![]() 时,由
时,由![]() ,推出
,推出![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
(2)如图②中,连接![]() 交
交![]() 于
于![]() 只要证明
只要证明![]() ,推出
,推出![]() ,可得
,可得![]() ,
,![]() ,推出
,推出![]() ,即
,即![]() ;
;
解:(1)①![]() ,
,
![]() 当
当![]() 时,有
时,有![]() ,即
,即![]() ①
①
![]() ②
②
由①②可得![]() ,
,![]() .
.
当![]() 时,有
时,有![]() ,
,![]() ,即
,即![]() ③
③
![]() ④,
④,
由③④可得![]() ,
,![]() .
.
综上所述,当![]() ,
,![]() 或
或![]() ,
,![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等;
全等;
②![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
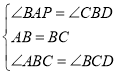 ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ;
;
(2)![]() 当
当![]() ,
,![]() 时,
时,![]() ,而
,而![]() ,
,
![]() ,
,
![]() 点
点![]() 在点
在点![]() 、
、![]() 之间,
之间,
![]() ,
,![]() ,
,
![]() ,
,
如图②中,连接![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
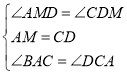 ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
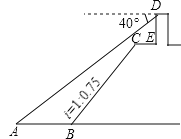
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于⊙O,A是
 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且 .
.(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明
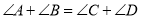 ;
;
【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:

①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =
 (∠B+∠D)=26°.
(∠B+∠D)=26°.【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想
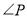 的度数,并说明理由.
的度数,并说明理由.
【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=
 ∠CAB,∠CDP=
∠CAB,∠CDP= ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
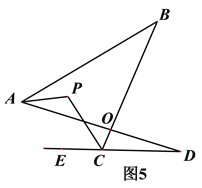
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
相关试题

