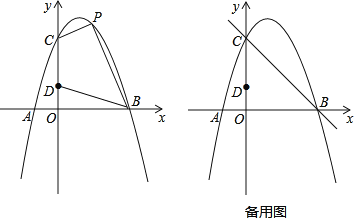
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
参考答案:
【答案】(1)y=﹣x2+2x+3(2)①t=![]() 时,S的最大值为
时,S的最大值为![]() ②P(1,4)或(2,3)或(
②P(1,4)或(2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)设所求抛物线的表达式为 y=a(x+1)(x﹣3),把点C(0,3)代入表达式,即可求解;
(2)①设P(t,﹣t2+2t+3),则E(t,﹣t+3),S四边形CDBP=S△BCD+S△BPC=![]() CDOB+
CDOB+![]() PEOB,即可求解;
PEOB,即可求解;
②分点P在点Q上方、下方两种情况讨论即可求解.
(1)∵抛物线的对称轴为x=1,A(﹣1,0),
∴B(3,0).
∴设所求抛物线的表达式为 y=a(x+1)(x﹣3),
把点C(0,3)代入,得3=a(0+1)(0﹣3),
解得a=﹣1,
∴所求抛物线的表达式为y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3;
(2)①连结BC.
∵B(3,0),C(0,3),
∴直线BC的表达式为y=﹣x+3,
∵OB=3OD,OB=OC=3,
∴OD=1,CD=2,
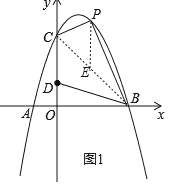
过点P作PE∥y轴,交BC于点E(如图1).
设P(t,﹣t2+2t+3),则E(t,﹣t+3).
∴PE=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t.
S四边形CDBP=S△BCD+S△BPC=![]() CDOB+
CDOB+![]() PEOB,
PEOB,
即S=![]() ×2×3+
×2×3+![]() (﹣t2+3t)×3=﹣
(﹣t2+3t)×3=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,且0<t<3,
<0,且0<t<3,
∴当t=![]() 时,S的最大值为
时,S的最大值为![]() ;
;
②以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,
则PQ∥CD,且PQ=CD=2.
∵点P在抛物线上,点Q在直线BC上,
∴点P(t,﹣t2+2t+3),点Q(t,﹣t+3).
分两种情况讨论:
(Ⅰ) 如图2,当点P在点Q上方时,
∴(﹣t2+2t+3)﹣(﹣t+3)=2.即t2﹣3t+2=0.解得 t1=1,t2=2.
∴P1(1,4),P2(2,3),
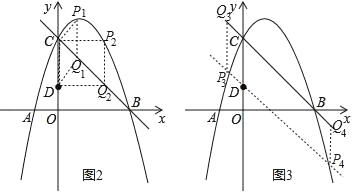
(Ⅱ) 如图3,当点P在点Q下方时,
∴(﹣t+3)﹣(﹣t2+2t+3)=2.即t2﹣3t﹣2=0.
解得 t3=![]() ,t4=
,t4=![]() ,
,
∴P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ),
),
综上所述,所有符合条件的点P的坐标分别为:P(1,4)或(2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
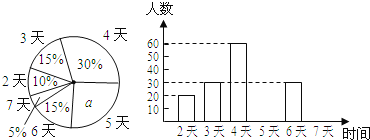
查看答案和解析>>【题目】江都区教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)扇形统计图中a=____ ___,参加调查的八年级学生人数为___ __人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为____ ___;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
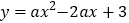 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与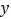 轴的交点为
轴的交点为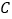 ,顶点为
,顶点为 .
.(1)求该二次函数的解析式及点
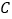 ,
, 的坐标;
的坐标;(2)点
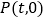 是
是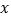 轴上的动点,
轴上的动点,①求
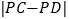 的最大值及对应的点
的最大值及对应的点 的坐标;
的坐标;②设
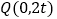 是
是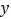 轴上的动点,若线段
轴上的动点,若线段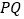 与函数
与函数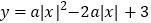 的图像只有一个公共点,求
的图像只有一个公共点,求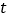 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
相关试题

