【题目】如图,![]() 中,
中,![]() ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:
①作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ;
;
②作边![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ;
;
③连接![]() ,
,![]() .
.
请你观察图形解答下列问题:

(1)线段![]() ,
,![]() ,
,![]() 之间的数量关系是________;
之间的数量关系是________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)![]() ;(2)80°.
;(2)80°.
【解析】(1)根据线段的垂直平分线的性质可得:PA=PB=PC;
(2)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°-2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
(1)如图,PA=PB=PC,理由是:
∵AB=AC,AM平分∠BAC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EP是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC;
故答案为:PA=PB=PC;
(2)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°-2×70°=40°,
∵AM平分∠BAC,
∴∠BAD=∠CAD=20°,
∵PA=PB=PC,
∴∠ABP=∠BAP=∠ACP=20°,
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以正方形
 的四条边为边,向其内部作等边三角形,得到
的四条边为边,向其内部作等边三角形,得到 、
、 、
、 、
、 ,连接
,连接 、
、 、
、 、
、 ,若
,若 ,则四边形
,则四边形 的面积为________.
的面积为________.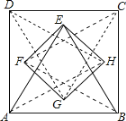
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 的面积为
的面积为 ,对角线
,对角线 ,
, 交于点
交于点 ,点
,点 ,
, ,
, ,
, 分别是
分别是 ,
, ,
,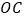 ,
, 的中点,连接
的中点,连接 ,
, ,
, ,
, 得到菱形
得到菱形 ;点
;点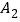 ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点,连接
的中点,连接 ,
, ,
, ,
, ,得到菱形
,得到菱形 ;…,依此类推,则菱形
;…,依此类推,则菱形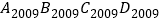 的面积为________.
的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
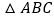 中,
中, ,
, ,
,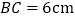 ,若动点
,若动点 从点
从点 开始,按
开始,按 的路径
的路径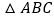 运动一周,且速度为每秒
运动一周,且速度为每秒 ,设运动的时间为
,设运动的时间为 秒.
秒.(
 )求
)求 为何值时,
为何值时, 把
把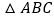 的周长分成相等的两部分
的周长分成相等的两部分(
 )求
)求 为何值时,
为何值时, 把
把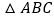 的面积分成相等的两部分;并求此时
的面积分成相等的两部分;并求此时 的长.
的长.(
 )求
)求 为何值时,
为何值时, 为等腰三角形?(请直接写出答案)
为等腰三角形?(请直接写出答案)

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 中,
中, 为
为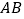 中点、
中点、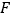 为
为 中点,
中点, 为
为 延长线上一点,连接
延长线上一点,连接 并延长交
并延长交 与点
与点 ,连接
,连接 ,求证:
,求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边
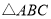 的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线
的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线 是经过点P的一条直线,把
是经过点P的一条直线,把 沿直线
沿直线 折叠,点B的对应点是点
折叠,点B的对应点是点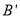 .
.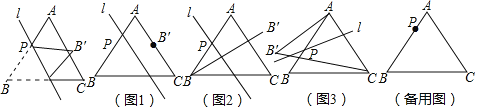
(1)如图1,当
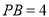 时,若点
时,若点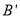 恰好在AC边上,则
恰好在AC边上,则 的长度为 ;
的长度为 ;(2)如图2,当
 时,若直线
时,若直线 ,则
,则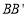 的长度为 ;
的长度为 ;(3)如图3,点P在AB边上运动过程中,若直线
 始终垂直于AC,
始终垂直于AC, 的面积是否变化?若变化,说明理由;若不变化,求出面积;
的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)当
 时,在直线
时,在直线 变化过程中,求
变化过程中,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 平分
平分 ,
, ,分别交
,分别交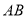 ,
, ,
, ,
, 的延长线于
的延长线于 ,
, ,
, ,
, ,已知下列四个式子:①
,已知下列四个式子:① ;②
;② ;③
;③ ;④
;④ .其中正确的式子有__________(填写序号).
.其中正确的式子有__________(填写序号).
相关试题

