【题目】如图,已知等边![]() 的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线
的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线![]() 是经过点P的一条直线,把
是经过点P的一条直线,把![]() 沿直线
沿直线![]() 折叠,点B的对应点是点
折叠,点B的对应点是点![]() .
.
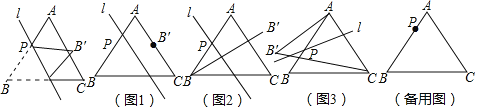
(1)如图1,当![]() 时,若点
时,若点![]() 恰好在AC边上,则
恰好在AC边上,则![]() 的长度为 ;
的长度为 ;
(2)如图2,当![]() 时,若直线
时,若直线![]() ,则
,则![]() 的长度为 ;
的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线![]() 始终垂直于AC,
始终垂直于AC,![]() 的面积是否变化?若变化,说明理由;若不变化,求出面积;
的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)长度为4;(2)长度为5![]() ;(3)△
;(3)△![]() 的面积不变化为16
的面积不变化为16![]() ,理由见解析;(4)△
,理由见解析;(4)△![]() 的面积的最大值为24+4
的面积的最大值为24+4![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接![]() ,由于折叠则△
,由于折叠则△![]() 为等边三角形,即可求出
为等边三角形,即可求出![]() 的长度;(2)记
的长度;(2)记![]() 与BC交于点D,连接
与BC交于点D,连接![]() 和
和![]() ,△BPD和△
,△BPD和△![]() 为边长等于5的等边三角形,所以
为边长等于5的等边三角形,所以![]() 为两边长为5的等边三角形的高之和,求出即可;(3)因为
为两边长为5的等边三角形的高之和,求出即可;(3)因为![]() ⊥AC,
⊥AC, ![]() ∥
∥![]() ,则
,则![]() 到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),![]() 的面积和△ABC的面积相等,算出即可;(4)由题意知
的面积和△ABC的面积相等,算出即可;(4)由题意知![]() =PB=6,所以
=PB=6,所以![]() 始终在以P点为圆心,6为半径的圆上运动,要使得△
始终在以P点为圆心,6为半径的圆上运动,要使得△![]() 面积最大,只要AC边上的高
面积最大,只要AC边上的高![]() 最大,如图,当
最大,如图,当![]() 经过圆心P时,
经过圆心P时,![]() 最大,算出其面积即可.
最大,算出其面积即可.
(1)连接![]() ,
,
∵等边![]() 的边长为8,PB=4,
的边长为8,PB=4,
∴AP=![]() =4,∠PAC=60°,
=4,∠PAC=60°,
∴△![]() 为等边三角形,
为等边三角形,
∴![]() =4;
=4;
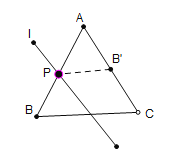
(2)记![]() 与BC交于点D,连接
与BC交于点D,连接![]() 和
和![]() ,
,
∵![]() ∥BC,
∥BC,![]() =BP=5,
=BP=5,
∴△BPD为边长等于5的等边三角形,
所以PD=![]() =5,∠
=5,∠![]() =∠BPD=60°,
=∠BPD=60°,
∴△![]() 为边长等于5的等边三角形,
为边长等于5的等边三角形,
由折叠知![]() ⊥
⊥![]() ,
,
∴![]() 为两边长为5的等边三角形的高之和,
为两边长为5的等边三角形的高之和,
则![]() =
=![]() ;
;

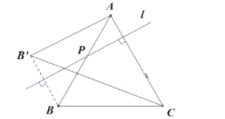
(3)△![]() 的面积不变化,理由如下:
的面积不变化,理由如下:
∵![]() ⊥AC,
⊥AC, ![]() ∥
∥![]() ,
,
∴![]() 到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
到AC的距离始终等于B到AC的距离(平行线之间的距离处处相等),
∴S△ACB’=S△ABC=![]() ×82=
×82=![]() ;
;
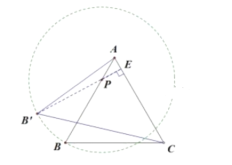
(4)由题意知![]() =PB=6,所以
=PB=6,所以![]() 始终在以P点为圆心,6为半径的圆上运动,要使得△
始终在以P点为圆心,6为半径的圆上运动,要使得△![]() 面积最大,只要AC边上的高
面积最大,只要AC边上的高![]() 最大,如图,当
最大,如图,当![]() 经过圆心P时
经过圆心P时![]() 最大,
最大,
∵∠BAC=60°,
∴AE=![]() AP=1,PE=
AP=1,PE=![]() AE=
AE=![]() ,
,![]() =
=![]() +6,
+6,
此时S△ACB’的最大值为![]() ×AC×
×AC×![]() =
=![]() ×8×(
×8×(![]() +6)=
+6)=![]() +24
+24
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
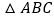 中,
中, ,
, ,
,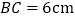 ,若动点
,若动点 从点
从点 开始,按
开始,按 的路径
的路径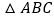 运动一周,且速度为每秒
运动一周,且速度为每秒 ,设运动的时间为
,设运动的时间为 秒.
秒.(
 )求
)求 为何值时,
为何值时, 把
把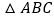 的周长分成相等的两部分
的周长分成相等的两部分(
 )求
)求 为何值时,
为何值时, 把
把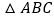 的面积分成相等的两部分;并求此时
的面积分成相等的两部分;并求此时 的长.
的长.(
 )求
)求 为何值时,
为何值时, 为等腰三角形?(请直接写出答案)
为等腰三角形?(请直接写出答案)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:①作
 的平分线
的平分线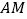 交
交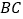 于点
于点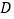 ;
;②作边
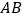 的垂直平分线
的垂直平分线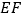 ,
,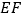 与
与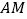 相交于点
相交于点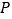 ;
;③连接
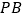 ,
,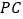 .
.请你观察图形解答下列问题:

(1)线段
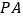 ,
,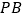 ,
,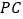 之间的数量关系是________;
之间的数量关系是________;(2)若
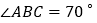 ,求
,求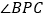 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 中,
中, 为
为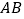 中点、
中点、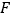 为
为 中点,
中点, 为
为 延长线上一点,连接
延长线上一点,连接 并延长交
并延长交 与点
与点 ,连接
,连接 ,求证:
,求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 平分
平分 ,
, ,分别交
,分别交 ,
, ,
, ,
, 的延长线于
的延长线于 ,
, ,
, ,
, ,已知下列四个式子:①
,已知下列四个式子:① ;②
;② ;③
;③ ;④
;④ .其中正确的式子有__________(填写序号).
.其中正确的式子有__________(填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接
 ,作
,作 的垂直平分线
的垂直平分线 分别交
分别交 ,
, ,
, 于
于 ,
, ,
, ,连接
,连接 ,
, ,则四边形
,则四边形 是菱形.
是菱形.乙:分别作
 ,
, 的平分线
的平分线 ,
, ,分别交
,分别交 ,
, 于
于 ,
, ,连接
,连接 ,则四边形
,则四边形 是菱形.
是菱形.根据两人的作法可判断( )

A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
 的正方形
的正方形 的对角线交于点
的对角线交于点 ,把边
,把边 、
、 分别绕点
分别绕点 、
、 同时逆时针旋转
同时逆时针旋转 得四边形
得四边形 ,其对角线交点为
,其对角线交点为 ,连接
,连接 .下列结论:
.下列结论:
①四边形
 为菱形;
为菱形;②
 ;
;③线段
 的长为
的长为 ;
;④点
 运动到点
运动到点 的路径是线段
的路径是线段 .其中正确的结论共有( )
.其中正确的结论共有( )A. 1个 B. 2个 C. 3个 D. 4个
相关试题

