【题目】已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8![]() ),点P从点C开始以每秒
),点P从点C开始以每秒![]() 个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.

(1)直接写出点A的坐标;
(2)求t为何值时,直线PQ与菱形ABCO的边互相垂直;
(3)如果将题中的条件变为点P的速度为每秒1个单位,点Q的速度为每秒a(1≤a≤3)单位,设运动时间为t(0<t≤8),其它条件不变.当a为何值时,以O,Q,D为顶点的三角形与△OAB相似?请给出你的结论,并加以证明.
参考答案:
【答案】(1)A(4,4![]() ).(2)t=2,t=8;(3)3.
).(2)t=2,t=8;(3)3.
【解析】
试题分析:(1)连接AC交OB于点M,根据菱形的性质,在RT△AMO中,求出AM、OM即可.
(2)分两种情形①如图1中,当PQ⊥OA时,过C作CH⊥OA于H,②如图2中,当PQ⊥AB时,过P作PN∥AB交射线OA于N,分别利用直角三角形30度性质列出方程即可解决.
(3)当a=1,a=3时,以O,Q,D为顶点的三角形与△OAB相似,①当a=1,△ODQ∽△OBA,②a=3时,△ODQ∽△OAB分别根据相似三角形性质列出方程即可解决.
试题解析:(1)连接AC交OB于点M,
∵∠AOC=60°,四边形ABCO是菱形,
∴AC垂直平分OB,OM=![]() OB=4
OB=4![]() ,∠AOM=30°,
,∠AOM=30°,
∴AM=4,
∴点D坐标为A(4,4![]() ).
).
(2)①如图1中,当PQ⊥OA时,过C作CH⊥OA于H,
∵PQ∥CH,PC∥QH,
∴四边形PCHQ是平行四边形,
∵∠CHQ=90°,
∴四边形PCHQ是矩形,
∴PC=QH=t,OQ=3t,∠OCH=30°,OH=2t=![]() OC=4,
OC=4,
∴t=2.
②如图2中,当PQ⊥AB时,过P作PN∥AB交射线OA于N,
由菱形ABCO得,PN=AB=8,
∴OQ=3t,CP=t,∠PQN=30°,NQ=2t=16,
∴t=8,
即当t=2,t=8时,直线PQ与菱形ABCO的边互相垂直.
(3)当a=1,a=3时,以O,Q,D为顶点的三角形与△OAB相似,
①当a=1,△ODQ∽△OBA,
证明:由△ODQ∽△OBA,可得∠ODQ=∠OBA,此时PQ∥AB,
∴四边形PCOQ为平行四边形,
∴CP=OQ,即at=t,(0<t≤8)
∴a=1时,△ODQ∽△OBA,
②a=3时,△ODQ∽△OAB
当P与B重合时,D点也与B重合,此时t=8,
由△ODQ∽△OAB,得
![]() ,
,
∵OD=OB,
∴OB2=OAOQ,
即(8![]() )2=8×8a,
)2=8×8a,
∴a=3,
∴a=3,△ODQ∽△OAB.


-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据1、3、4、5、x、9的众数和中位数相同,那么x的值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a+b)2=16,ab=4,求a2+b2与(a-b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2﹣2x+m=0的一个根为﹣1,则另一个根为( )
A. ﹣3B. ﹣1C. 1D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
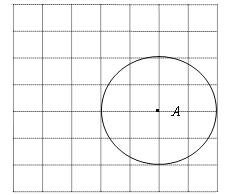
(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移____________个单位长度与y轴首次相切,得到⊙A,并画出⊙A.此时点A的坐标为_____________.
(3)求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(k﹣2)x+k+1的图象不过第三象限,则k的取值范围是( )
A. k>2B. k<2C. ﹣1≤k≤2D. ﹣1≤k<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于抛物线y=(x+1)2+3有以下结论:①抛物线开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小.其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
相关试题

