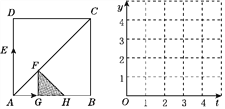
【题目】如图,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?
参考答案:
【答案】(1)![]() ;
; ![]() ;(2)当t=
;(2)当t=![]() 或t=4时,四边形DEGF是平行四边形.
或t=4时,四边形DEGF是平行四边形.
【解析】试题分析:(1)当t=1.5时,如图①,重叠部分的面积是△FGH的面积,求出即可;当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,求出即可;
(2)进行分类讨论,列出方程即可求出t的值.
试题解析:当t=1.5时,如图①,重叠部分的面积是△FGH的面积,所以S=![]() ;
;
当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,所以S=![]() ×3×3-
×3×3-![]() ×2×2=
×2×2=![]() .
.
(2)由题意可以求得
y1= ![]() ;y2=t(0≤t≤4).<
;y2=t(0≤t≤4).<
所以y1与y2关于t的函数图象如图③所示.
因为运动过程中,DE∥FG,所以当DE=FG时,四边形DEGF是平行四边形.
∵FG=AG,
∴DE=AG,
∴y1=y2.由图象可知,有两个t值满足条件:
①当0≤t≤2时,由4-2t=t,解得t=![]() ;
;
②当2<t≤4时,由2t-4=t,解得t=4.
所以当t=![]() 或t=4时,四边形DEGF是平行四边形.
或t=4时,四边形DEGF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂重量x(kg)
0
1
2
3
4
5
弹簧长度y(cm)
18
20
22
24
26
28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式,并求出当所挂重物为6kg时,弹簧的长度为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图
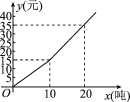
(1)求a的值,某户居民上月用水8吨,应收水费多少元;
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
-
科目: 来源: 题型:
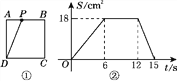
查看答案和解析>>【题目】如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,三角形APD的面积为10 cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一名学生所做的4道练习题:①﹣22=4②a3+a3=a6③4m﹣4=
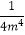 ④(xy2)3=x3y6 , 他做对的个数( )
④(xy2)3=x3y6 , 他做对的个数( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x2﹣7x+3=0
(2)x(x﹣2)=x. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣(x+h)2 , 当x<﹣3时,y随x的增大而增大,当x>﹣3时,y随x的增大而减小,当x=0时,y的值为( )
A.﹣1
B.﹣9
C.1
D.9
相关试题

