搜索
【题目】已知在△ABC中，试说明：∠A+∠B+∠C=180°
方法一： 过点A作DE∥BC. 则（填空）
∠B=∠ ，∠C=∠
∵ ∠DAB+∠BAC+ ∠CAE=180°
∴∠A+∠B+∠C=180°
方法二： 过BC上任意一点D作DE∥AC，DF∥AB分别交AB、AC于E、F（补全说理过程 ）
参考答案：
【答案】DAB，CAE ；见解析
【解析】
方法一：根据平行线的性质：两直线平行，内错角相等解答；
方法二：根据平行线的性质：两直线平行、同位角相等解答.
方法一：∵DE∥BC,
∴∠B=∠DAB，∠C=∠CAE，
故答案为：DAB，CAE ；
方法二：∵DE∥AC，
∴∠A=∠BED，∠C=∠BDE，
∵DF∥AB，
∴∠EDF=∠BED，∠B=∠CDF，
∵∠CDF+∠EDF+∠BDE=180°，
∴∠A+∠B+∠C=180°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数
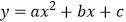的图象如图所示，反比例函数 
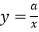与正比例函数 
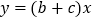在同一坐标系中的大致图象可能是（ ）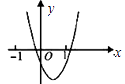
A.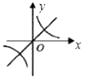
B.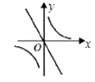
C.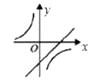
D.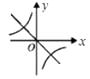
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，
，点D在BC所在的直线上，点E在射线AC上，且
，连接DE．（1）如图①，若
， 
，求
的度数；（2）如图②，若
， 
，求
的度数；（3）当点D在直线BC上（不与点B、C重合）运动时，试探究
与
的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠BOC=9°，点A在OB上，且OA=1，按下列要求画图：
以A为圆心，1为半径向右画弧交OC于点A1，得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2，得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3，得第3条线段A2A3；…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n=______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF（顶点为网格线的交点），以及过格点的直线l．
（1）将△ABC向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形．
（2）画出△DEF关于直线l对称的三角形．
（3）填空：∠C+∠E＝ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．
（1）求证：DE=DF，DE⊥DF；
（2）连接EF，若AC=10，求EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题1：现有一张△ABC纸片，点D、E分别是△ABC边上两点，若沿直线DE折叠．
（1）探究1：如果折成图①的形状，使A点落在CE上，则∠1与∠A的数量关系是 ；
（2）探究2：如果折成图②的形状，猜想∠1+∠2和∠A的数量关系是 ；
（3）探究3：如果折成图③的形状，猜想∠1、∠2和∠A的数量关系，并说明理由．
（4）问题2：将问题1推广，如图④，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是 .
相关试题
