搜索
【题目】七年级一班某次数学测验的优秀成绩为80分，数学老师以优秀成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分？优秀率是多少？
参考答案：
【答案】（1）90分，65分，80分，100分，78分；（2）优秀率为60%.
【解析】
（1）分别用基准分加上简记的数，即可得出成绩；
（2）用大于等于80分的人数除以总人数得到优秀率.
解：（1）80+10=90，80-15=65，80+0=80，80+20=100，80-2=78，
答：这五位同学的实际成绩分别是：90分，65分，80分，100分，78分.
（2）因为大于等于80分的有3人，所以优秀率为
，
答：优秀率为60%.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（∠M＝30°）的直角项点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
（1）将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周．如图2，经过t秒后，ON落在OC边上，则t＝ 秒（直接写结果）．
（2）在（1）的条件下，若三角板继续转动，同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周，当OC转动9秒时，求∠MOC的度数．
（3）在（2）的条件下，它们继续运动多少秒时，∠MOC＝35°？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，点D，E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
（1）求证：CE是⊙O的切线；
（2）若BF=2，EF=
，求⊙O的半径长．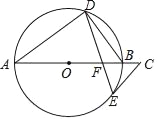
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下面左边
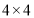方格中，都有两个形状、大小相同的直角三角形①、②，它们的顶点都在小正方形的顶点处（在方格中，三个顶点都在小正方形的顶点处的三角形叫做格点三角形）．图中只有直角三角形①可以运动．按下列要求在右边的备用图中画出运动后的图形．（注：一个
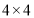方格中只画一种情况，给出的备用图不一定全用，不够可添加）（1）如图一，只通过平移直角三角形①，使平移后的图形与直角三角形②成旋转对称图形，请你画出所有与三角形②成旋转对称的格点三角形，并分别写出平移的方向及距离．
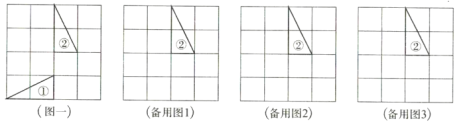
（2）如图二，只通过旋转直角三角形①（绕着它的顶点），使旋转后的图形与直角三角形②成轴对称图形，请你画出所有与三角形②成轴对称的格点三角形，并分别写出旋转的方向及旋转角，在图中标出旋转中心
．
-
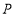科目： 来源： 题型：
查看答案和解析>>【题目】定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．
应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
（1）求证：△AOB和△AOE是“友好三角形”；
（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．
探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的
，请直接写出△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一家水果店以每千克2元的价格购进某种水果若干千克，然后以每千克4元的价格出售，每天可售出100千克，通过调查发现，这种水果每千克的售价每降低1元，每天可多售出200千克．
（1）若将这种水果每千克的售价降低
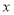元，则每天销售量是多少千克？（结果用含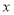的代数式表示）（2）若想每天盈利300元，且保证每天至少售出260千克，那么水果店需将每千克的售价降低多少元？
-
科目： 来源： 题型：
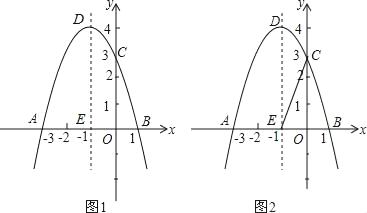
查看答案和解析>>【题目】如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．
（1）求抛物线的解析式；
（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；
（3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．
相关试题
