【题目】如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点. 
(Ⅰ)求r的取值范围;
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.
参考答案:
【答案】解:(Ⅰ)将抛物线E:y2=x代入圆M:(x﹣4)2+y2=r2(r>0)的方程, 消去y2 , 整理得x2﹣7x+16﹣r2=0(1)
抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:
方程(1)有两个不相等的正根
∴ 
即  .
.
解这个方程组得 ![]() ,
,  .
.
(II)设四个交点的坐标分别为![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .
.
则直线AC、BD的方程分别为y﹣ ![]() =
=  (x﹣x1),y+
(x﹣x1),y+ ![]() =
=  (x﹣x1),
(x﹣x1),
解得点P的坐标为( ![]() ,0),
,0),
则由(I)根据韦达定理有x1+x2=7,x1x2=16﹣r2 , 
则 ![]()
∴ ![]()
令 ![]() ,
,
则S2=(7+2t)2(7﹣2t)下面求S2的最大值.
由三次均值有: ![]() 当且仅当7+2t=14﹣4t,即
当且仅当7+2t=14﹣4t,即 ![]() 时取最大值.
时取最大值.
经检验此时  满足题意.
满足题意.
故所求的点P的坐标为 ![]() .
.
【解析】(1)先联立抛物线与圆的方程消去y,得到x的二次方程,根据抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x2﹣3)ex , 设关于x的方程
 有n个不同的实数解,则n的所有可能的值为( )
有n个不同的实数解,则n的所有可能的值为( )
A.3
B.1或3
C.4或6
D.3或4或6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
 ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
,DC=SD=2,点M在侧棱SC上,∠ABM=60°. 
(Ⅰ)证明:M是侧棱SC的中点;
(Ⅱ)求二面角S﹣AM﹣B的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名维修工人进行维修,每台机器出现故障需要维修的概率为
 . (Ⅰ)若出现故障的机器台数为x,求x的分布列;
. (Ⅰ)若出现故障的机器台数为x,求x的分布列;
(Ⅱ)该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(Ⅲ)已知一名维修工人每月只有维修1台机器的能力,每月需支付给每位维修工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名维修工人,求该厂每月获利的均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
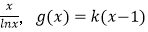 .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ 成立,求实数k的取值范围.
成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xoy中,已知点P(0,
 ),曲线C的参数方程为
),曲线C的参数方程为  (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=  . (Ⅰ)判断点P与直线l的位置关系并说明理由;
. (Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求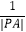 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围.
相关试题

