【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围.
参考答案:
【答案】
(1)解:依题意有:|2a﹣3|<|a|﹣(a﹣3),
若a≥ ![]() ,则2a﹣3<3,∴
,则2a﹣3<3,∴ ![]() ≤a<3,
≤a<3,
若0≤a< ![]() ,则3﹣2a<3,∴0<a<
,则3﹣2a<3,∴0<a< ![]() ,
,
若a≤0,则3﹣2a<﹣a﹣(a﹣3),无解,
综上所述,a的取值范围为(0,3)
(2)解:由题意可知,当x∈[﹣1,1]时,f(x)<g(x)恒成立,
∴|x+a|<3恒成立,
即﹣3﹣x<a<3﹣x,当x∈[﹣1,1]时恒成立,
∴﹣2<a<2
【解析】(1)将x=a﹣3代入不等式,解关于a的不等式即可;(2)得到|x+a|<3恒成立,即﹣3﹣x<a<3﹣x,当x∈[﹣1,1]时恒成立,求出a的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.

(Ⅰ)求r的取值范围;
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
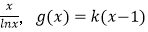 .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ 成立,求实数k的取值范围.
成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xoy中,已知点P(0,
 ),曲线C的参数方程为
),曲线C的参数方程为  (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=  . (Ⅰ)判断点P与直线l的位置关系并说明理由;
. (Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求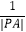 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行右面的程序框图,如果输入的N=10,那么输出的S=( )

A.
B.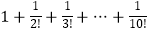
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移
 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ,
,  ]上单调递减
]上单调递减
B.在区间[﹣ ,
,  ]上单调递增
]上单调递增
C.在区间[﹣ ,
,  ]上单调递减
]上单调递减
D.在区间[﹣ ,
,  ]上单调递增
]上单调递增 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为
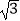 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 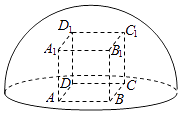
A.1
B.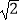
C.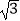
D.2
相关试题

