【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
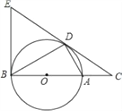
(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见解析;(2) BE的长为5.
【解析】试题分析: (1)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可.(2)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可.
试题解析:
(1)证明:连OD,OE,如图,∵AB为直径,∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,而∠CBD=∠1,∴∠1=∠CDA,∴∠CDA+∠ADO=90°,即∠CDO=90°,∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,∴ED=EB,OE⊥DB,∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,∴∠CDA=∠OEB.而tan∠CDA=![]() ,∴tan∠OEB=
,∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,(1)证明:连OD,OE,如图,
∵AB为直径,∴∠ADB=90°,即∠ADO+∠1=90°,又∵∠CDA=∠CBD,而∠CBD=∠1,∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,∴CD是⊙O的切线;∴![]()
![]() ,∴CD=
,∴CD=![]() ×12=8,
×12=8,
在Rt△CBE中,设BE=x,∴(x+8)2=x2+122,解得x=5.即BE的长为5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有男生30人,女生20人.下图分别是该班男、女生参加体育锻炼项目人数的扇形统计图.根据统计图,该班参加体育锻炼人数最多的项目是( )

A.跳绳
B.引体向上
C.跳远
D.仰卧起坐 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣
 x2+
x2+ x+4经过A、B两点.
x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨: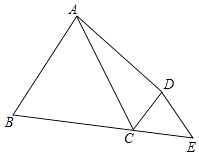
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= , 且CE=CD,可知;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即=;
请你先完成思路点拨,再进行证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 (k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算正确的是( )
A.(ab2)3=ab6 B.(3xy)2=6x2y2 C.(-2a2)2=-4a4 D.(a2b3)m=a2mb3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为6,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,现在有如下4个结论:①G、F、E三点共线;②BG=4;③△BEF∽△CDF;④S△BFG=
 .
.在以上4个结论中,正确的有 ________________(填番号).

相关试题

