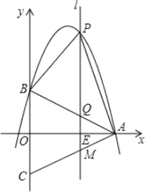
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(8,0)、B(0,4);(2)S=﹣8t2+32t+32,S最大值为64.(3)存在符合条件的点P,坐标为(3,10).
【解析】试题分析:(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(![]() PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.
PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.
试题解析:
(1)抛物线y=﹣0.5x2+3.5x+4中:令x=0,y=4,则 B(0,4);
令y=0,0=﹣0.5x2+3.5x+4,解得 x1=﹣1、x2=8,则 A(8,0);∴A(8,0)、B(0,4).
(2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,﹣4).
由A(8,0)、B(0,4),得:直线AB:y=﹣0.5x+4;
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;
S=S△ABC+S△PAB=0.5×8×8+0.5×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;
∴当t=2时,S有最大值,且最大值为64.
(3)∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,﹣4),得:直线AC:y=0.5x﹣4;
所以,直线AP可设为:y=﹣2x+h,代入A(8,0),得:﹣16+h=0,h=16
∴直线AP:y=﹣2x+16,联立抛物线的解析式,∴存在符合条件的点P,且坐标为(3,10).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
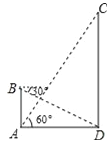
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人准备设计平行四边形图案,拟以长为4cm,5cm,7cm的三条线段中的两条为边,另一条为对角线画不同形状的平行四边形,他可以画出形状不同的平行四边形的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有男生30人,女生20人.下图分别是该班男、女生参加体育锻炼项目人数的扇形统计图.根据统计图,该班参加体育锻炼人数最多的项目是( )

A.跳绳
B.引体向上
C.跳远
D.仰卧起坐 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨: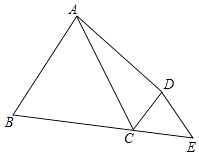
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= , 且CE=CD,可知;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即=;
请你先完成思路点拨,再进行证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
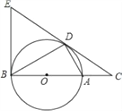
(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=
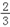 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 (k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

