【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

参考答案:
【答案】问题呈现:证明见解析;实验探究:结论:2S四边形EFGH=S矩形ABCD﹣![]() ;(3)
;(3)![]() .
.
【解析】试题分析:只要说明S△HGE=![]() S矩形AEGD,同理S△EGF=
S矩形AEGD,同理S△EGF=![]() S矩形BEGC,由此可得S四边形EFGH=S△HGE+S△EFG=
S矩形BEGC,由此可得S四边形EFGH=S△HGE+S△EFG=![]() S矩形ABCD;
S矩形ABCD;
实验探究:结论:2S四边形EFGH=S矩形ABCD-S矩形A1B1C1D1.根据S△EHC1=![]() S矩形AEC1H,S△HGD1=
S矩形AEC1H,S△HGD1=![]() S矩形HDGD1,S△EFB1=
S矩形HDGD1,S△EFB1=![]() S矩形EBFB1,S△FGA1=
S矩形EBFB1,S△FGA1=![]() S矩形CFA1G,即可证明;
S矩形CFA1G,即可证明;
迁移应用:利用探究的结论即可解决问题.
试题解析:
如图中,

∵四边形ABCD是矩形,
∴AB∥CD,∠A=90°,
∵AE=DG,
∴四边形AEGD是矩形,
∴S△HGE=![]() S矩形AEGD,
S矩形AEGD,
同理S△EGF=![]() S矩形BEGC,
S矩形BEGC,
∴S四边形EFGH=S△HGE+S△EFG=![]() S矩形ABCD.
S矩形ABCD.
故答案为:S四边形EFGH=![]() S矩形ABCD.
S矩形ABCD.
实验探究:结论:2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.

理由:∵S△EHC1=![]() S矩形AEC1H,S△HGD1=
S矩形AEC1H,S△HGD1=![]() S矩形HDGD1,S△EFB1=
S矩形HDGD1,S△EFB1=![]() S矩形EBFB1,S△FGA1=
S矩形EBFB1,S△FGA1=![]() S矩形CFA1G,
S矩形CFA1G,
∴S四边形EFGH=S△EHC1+S△HGD1+S△EFB1+S△FGA1﹣S矩形A1B1C1D1,
∴2S四边形EFGH=2S△EHC1+2S△HGD1+2S△EFB1+2S△FGA1﹣2S矩形A1B1C1D1,
∴2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.
故答案为:2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1
迁移应用:解:(1)如图中,

∵2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.
∴S矩形A1B1C1D1=25﹣2×9=7=A1B1A1D1,
∵正方形的面积为25,
∴边长为5,
∵A1D12=HF2﹣52=29﹣25=4,
∴A1D1=2,A1B1=![]() ,
,
∴EG2=A1B12+52=![]() ,
,
∴EG=![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣5.3)+(3.2)﹣(﹣2.5)﹣(+4.8)
(2)﹣2÷(﹣2
 )×(﹣4.5)
)×(﹣4.5)(3)﹣24×(
 )
) (4)﹣22﹣(﹣
 )3×8﹣4÷(﹣
)3×8﹣4÷(﹣ )2.
)2. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了美化校园环境,在一块长40米,宽20米的长方形空地上计划新建一块长9米,宽7米的长方形花圃.
(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多1平方米,请你给出你认为合适的三种不同的方案;
(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a、b、c三个数在数轴上位置如图所示,且|a|=|b|
(1)求出a、b、c各数的绝对值;
(2)比较a,﹣a、﹣c的大小;
(3)化简|a+b|+|a﹣b|+|a+c|+|b﹣c|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A,∠B,∠C的对边分别记为
 ,
, ,
, ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.

D.
 ∶
∶ ∶
∶ =3∶4∶6
=3∶4∶6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是( )cm.

A.7
B.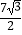
C.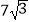
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到章丘某旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点,汽车匀速行驶
相关试题

