【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
参考答案:
【答案】B
【解析】
对于一元二次方程a(x-1)2+b(x-1)-1=0,设t=x-1得到at2+bt-1=0,利用at2+bt-1=0有一个根为t=2019得到x-1=2019,从而可判断一元二次方程a(x-1)2+b(x-1)=1必有一根为x=2020.
对于一元二次方程a(x-1)2+b(x-1)-1=0,
设t=x-1,
所以at2+bt-1=0,
而关于x的一元二次方程ax2+bx-1=0(a≠0)有一根为x=2019,
所以at2+bt-1=0有一个根为t=2019,
则x-1=2019,
解得x=2020,
所以一元二次方程a(x-1)2+b(x-1)=1必有一根为x=2020.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为20,对角线AC长为
 ,点E、F分别为AC、BC边上的动点.
,点E、F分别为AC、BC边上的动点.
(1)直接写出菱形ABCD的面积:_______;
(2)直接写出BE+EF的最小值_______;并在图中作出此时的点E和点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y= ax+bx+c,自变量x 与函数y 的对应值如表:
x
...
-5
-4
-3
-2
-1
0
...
y
...
4
0
-2
-2
0
4
...
下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是x=-5/2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴ ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A.
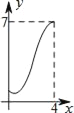 B.
B. 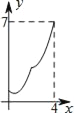 C.
C. 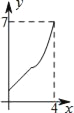 D.
D. 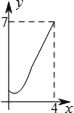
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一元二次方程
 中,若系数
中,若系数 和
和 可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数
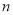 ,如果
,如果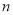 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”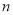 的各个数位上的数字之和记为
的各个数位上的数字之和记为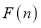 . 例如
. 例如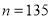 时,
时,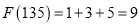 .
. (1)对于“相异数”
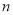 ,若
,若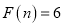 ,请你写出一个
,请你写出一个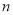 的值;
的值;(2)若
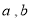 都是“相异数”,其中
都是“相异数”,其中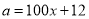 ,
,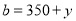 (
(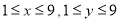 ,
,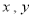 都是正整数),规定:
都是正整数),规定: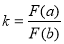 ,当
,当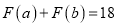 时,求
时,求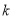 的最小值.
的最小值.
相关试题

