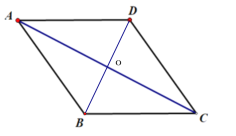
【题目】如图,菱形ABCD的周长为20,对角线AC长为![]() ,点E、F分别为AC、BC边上的动点.
,点E、F分别为AC、BC边上的动点.

(1)直接写出菱形ABCD的面积:_______;
(2)直接写出BE+EF的最小值_______;并在图中作出此时的点E和点F.
参考答案:
【答案】(1)20;(2)2![]() ,E、F两点的位置见解析.
,E、F两点的位置见解析.
【解析】
(1)如图:连接BD交AC于O点,再根据菱形的性质求出AB和OA的长,再利用勾股定理求得OB的长,进而求得BD的长,最后利用菱形的面积等于对角线积的一半解答即可;
(2)根据点到直线的距离垂线段最短,可确定当点E与点O重合时BE最短;当F与B重合时EF=OB取最小值,即 BE+EF=2OB=BD的长.
(1)解:连接BD交AC于O点,
∵菱形ABCD的周长为20,对角线AC=![]()
∴AB=5,OA=![]()
∴OB=![]() =
=![]()
∴BD=2![]()
∴菱形的面积为:![]() =20.
=20.
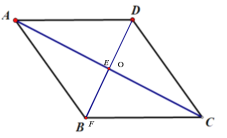
(2)解:当点E与点O重合时BE最短,BE=OB(垂线段最短);
当F与B重合时,EF=OB取最小值;
所以BE+EF=2OB=BD=2![]() ;
;
E、F的位置如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
1月
2月
3月
4月
5月
甲
9
9
8
7
5
乙
10
9
6
8
8
丙
11
10
5
5
9
(1)根据上表中的数据,将下表补充完整:
平均数
(万元)
众数
(万元)
中位数
(万元)
甲
7. 6
8
乙
8
8
丙
8
5
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于正数
 ,用符号
,用符号 表示
表示 的整数部分,例如:
的整数部分,例如: ,
, ,
,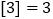 .点
.点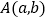 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于 轴的边长为
轴的边长为 ,垂直于
,垂直于 轴的边长为
轴的边长为 ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点 的矩形域是一个以
的矩形域是一个以 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.

图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是 ;
(2)点
 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求 的值;
的值; (3)已知点
 在直线
在直线 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积 满足
满足 ,那么
,那么 的取值范围是 .(直接写出结果)
的取值范围是 .(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
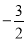 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
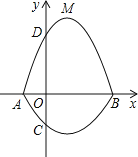
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y= ax+bx+c,自变量x 与函数y 的对应值如表:
x
...
-5
-4
-3
-2
-1
0
...
y
...
4
0
-2
-2
0
4
...
下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是x=-5/2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴ ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.
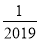 B.2020C.2019D.2018
B.2020C.2019D.2018
相关试题

