【题目】二次函数y= ax+bx+c,自变量x 与函数y 的对应值如表:
x | ... | -5 | -4 | -3 | -2 | -1 | 0 | ... |
y | ... | 4 | 0 | -2 | -2 | 0 | 4 | ... |
下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是x=-5/2
参考答案:
【答案】D
【解析】将点(4,0)、(1,0)、(0,4)代入到二次函数y=ax2+bx+c中,
得: 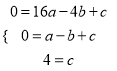 ,解得:
,解得: 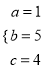 ,
,
∴二次函数的解析式为y=x +5x+4.
A.a=1>0,抛物线开口向上,A不正确;
B.![]() =
=![]() ,当x
,当x![]() 时,y随x的增大而增大,B不正确;
时,y随x的增大而增大,B不正确;
C.y=x+5x+4=(x+![]() )
) ![]() ,二次函数的最小值是
,二次函数的最小值是![]() ,C不正确;
,C不正确;
D.![]() =
=![]() ,抛物线的对称轴是x=
,抛物线的对称轴是x=![]() ,D正确.
,D正确.
故选D.
点睛: 本题主要考查二次函数的性质,利用待定系数法求得抛物线解析式是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于正数
 ,用符号
,用符号 表示
表示 的整数部分,例如:
的整数部分,例如: ,
, ,
,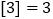 .点
.点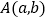 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于 轴的边长为
轴的边长为 ,垂直于
,垂直于 轴的边长为
轴的边长为 ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点 的矩形域是一个以
的矩形域是一个以 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.

图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是 ;
(2)点
 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求 的值;
的值; (3)已知点
 在直线
在直线 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积 满足
满足 ,那么
,那么 的取值范围是 .(直接写出结果)
的取值范围是 .(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
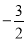 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
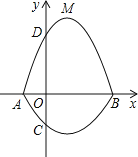
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为20,对角线AC长为
 ,点E、F分别为AC、BC边上的动点.
,点E、F分别为AC、BC边上的动点.
(1)直接写出菱形ABCD的面积:_______;
(2)直接写出BE+EF的最小值_______;并在图中作出此时的点E和点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴ ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.
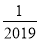 B.2020C.2019D.2018
B.2020C.2019D.2018 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
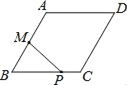
A.
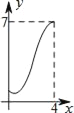 B.
B. 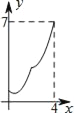 C.
C. 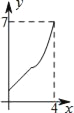 D.
D. 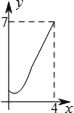
相关试题

