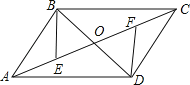
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF.
(1) 求证:△BOE≌△DOF;
(2) 连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
参考答案:
【答案】(1)见解析;(2)四边形EBDF为菱形,理由见解析
【解析】
(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;
(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
证明:(1) ∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中
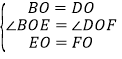 ,
,
∴△BOE≌△DOF(SAS);
(2) 四边形EBDF为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角、同旁内角;
(3)指出FB,BC被AC所截形成的内错角、同旁内角.

-
科目: 来源: 题型:
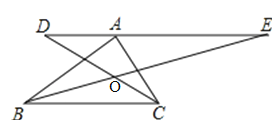
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=_____,DE的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x、y是实数,并且
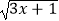 +y2﹣6y+9=0,则(xy)2017的值是 .
+y2﹣6y+9=0,则(xy)2017的值是 .
若一个等腰三角形的三边长均满足方程y2﹣6y+8=0,则此三角形的周长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
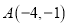 ,
,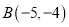 ,
,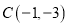 ,
,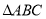 经过平移得到的
经过平移得到的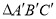 ,
,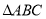 中任意一点
中任意一点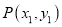 平移后的对应点为
平移后的对应点为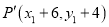 .
.(1)请在图中作出
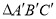 ;
;(2)写出点
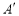 、
、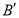 、
、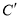 的坐标;
的坐标;(3)求
 的面积.
的面积.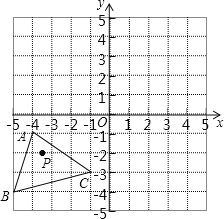
-
科目: 来源: 题型:
查看答案和解析>>【题目】“镇康人民想致富,可惜差条二级路”这一啊数瑟小调流传镇康大街小巷.经有关部门批准,龙南二级路已于 2015 年初启动,已知两工程队共同参与某项筑路工程,甲队单独施工一个月完成总工程的
 ,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:
,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:(1)那个工程队的施工速度快?
(2)若甲、乙两队同时施工,需多少时间完成整项工程?
相关试题

