【题目】如图,已知四边形ABCD中,∠B=60°,边AB=BC=8cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是每秒1cm,点Q运动的速度是每秒2cm,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
解答下列问题:
(1)AP= ,BP= ,BQ= .(用含t的代数式表示,t≤4)
(2)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(3)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.

参考答案:
【答案】(1)t,8﹣t,2t;(2)PQ⊥AB,理由见解析;(3)△BPQ能成为等边三角形,t=![]() .
.
【解析】
(1)根据点P、Q的运动速度解答;
(2)连接AC,得到△ABC为等边三角形,根据等腰三角形的三线合一证明;
(3)根据等边三角形的判定定理列出方程,解方程即可.
(1)由题意得:AP=t,BP=8﹣t,BQ=2t.
故答案为:t;8﹣t;2t;
(2)PQ⊥AB.理由如下:
连接AC.
∵∠B=60°,AB=BC,∴△ABC为等边三角形.
∵点Q到达点C时,BQ=BC=8cm,AP=4,∴P为AB的中点,∴PQ⊥AB;
(3)△BPQ能成为等边三角形.
∵∠B=60°,∴当BP=BQ时,△BPQ能成为等边三角形,此时,8﹣t=2t,解得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:跳绳,B:跑操,C:舞蹈,D:健美操共四项活动,为了了解学生最喜欢哪一种活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人.
(2)请将条形统计图补充完整.
(3)求出扇形统计图中A项目对应的圆心角的度数.
-
科目: 来源: 题型:
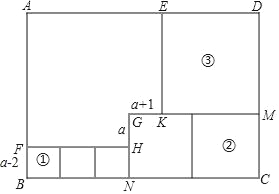
查看答案和解析>>【题目】如图所示,用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=a,GK=a+1,BF=a﹣2
(1)试用含a的代数式表示:正方形②的边长CM的长= ,正方形③的边长DM的长= ;
(2)求长方形ABCD的周长(用含a的代数式表示);并求出当a=3时,长方形周长的值.
-
科目: 来源: 题型:
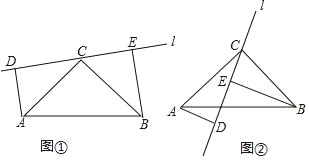
查看答案和解析>>【题目】探究:如图①,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的同侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.求证:DE=AD+BE.
应用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的异侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.直接写出线段AD、BE、DE之间的相等关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)计算: ;
;
(2)解分式方程: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克)
﹣4
﹣2
0
1
3
6
个数
10
13
30
25
15
7
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F是ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
相关试题

