【题目】计算下面各题
(1)计算: ![]() ;
;
(2)解分式方程: ![]() .
.
参考答案:
【答案】
(1)解:原式=1+2 ![]() ﹣
﹣ ![]() ,
,
=1+ ![]()
(2)解:2(x+3)=3(x﹣2),
解得:x=12,
检验:当x=12时,x﹣2=12﹣2=10≠0,
∴原方程的根是x=12
【解析】(1)根据零指数幂,以及特殊角的三角函数值即可解答本题,(2)观察方程可得最简公分母是:2(x﹣2),两边同时乘最简公分母可把分式方程化为整式方程来解答.
【考点精析】根据题目的已知条件,利用零指数幂法则和去分母法的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊.
-
科目: 来源: 题型:
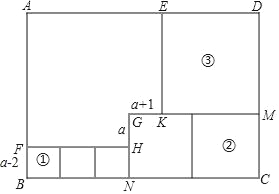
查看答案和解析>>【题目】如图所示,用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=a,GK=a+1,BF=a﹣2
(1)试用含a的代数式表示:正方形②的边长CM的长= ,正方形③的边长DM的长= ;
(2)求长方形ABCD的周长(用含a的代数式表示);并求出当a=3时,长方形周长的值.
-
科目: 来源: 题型:
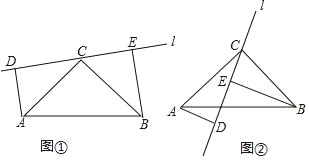
查看答案和解析>>【题目】探究:如图①,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的同侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.求证:DE=AD+BE.
应用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的异侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.直接写出线段AD、BE、DE之间的相等关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=60°,边AB=BC=8cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是每秒1cm,点Q运动的速度是每秒2cm,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
解答下列问题:
(1)AP= ,BP= ,BQ= .(用含t的代数式表示,t≤4)
(2)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(3)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克)
﹣4
﹣2
0
1
3
6
个数
10
13
30
25
15
7
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F是ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣20)+(+3)﹣(﹣5)
(2)(﹣5)×6×
 ÷(﹣2)
÷(﹣2)(3)﹣
 ÷
÷ ﹣
﹣ ×(﹣9)
×(﹣9)(4)(﹣1)4+5÷(﹣
 )×(﹣6)
)×(﹣6)(5)(
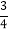 +
+ ﹣
﹣ )×36
)×36(6)﹣1﹣[1
 +(﹣12)÷6]×(﹣
+(﹣12)÷6]×(﹣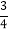 )
)
相关试题

