【题目】如图,△ABC中,AB=AC=10,BC=12,点D在边BC上,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交AC或延长线于点F. 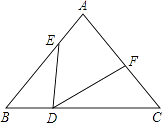
(1)当AE=4时,求AF的长;
(2)当以边AC为直径的⊙O与线段DE相切时,求BE的长.
参考答案:
【答案】
(1)解:∵∠EDF+∠FDC=∠B+∠DEB,∠EDF=∠B,
∴∠FDC=∠DEB,
∵AB=AC,
∴∠C=∠B,
∴△CDF∽△BED,
∴ ![]() ,即
,即 ![]() ,
,
解得:CF= ![]() ,
,
∴AF=AC﹣CF=10﹣ ![]()
(2)解:取边AC中点O,作OG⊥DE于G,OQ⊥BC于Q,过点A作AH⊥BC于H,连接OD,如图所示:
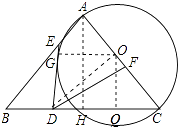
∵AB=AC,AH⊥BC,
∴CH= ![]() BC=6,
BC=6,
∵⊙O和线段DE相切,
∴OG= ![]() AC=5,
AC=5,
在Rt△CAH中,∠AHC=90°,cosC= ![]() ,
,
在Rt△CQO中,∠CQO=90°
∵cosC= ![]() ,
,
∴CQ=COcosC=5× ![]() =3,
=3,
∴DQ=BC﹣BD﹣CQ=12﹣4﹣3=5,
∴OG=DQ,
在Rt△OGD与Rt△DQO中, ![]() ,
,
∴Rt△OGD≌Rt△DQO(HL),
∴∠GOD=∠QDO,
∴OG∥BC,
∴∠EDB=∠OGD=90°,
∴cosB= ![]() =cosC=
=cosC= ![]() ,
,
∴BE= ![]() ,
,
∴当以边AC为直径的⊙O与线段DE相切时,BE= ![]() .
.
【解析】(1)先证△BDE∽△CFD,得出对应边成比例,求出CF的长,即可得出结果;(2)取边AC中点O,作OG⊥DE于G,OQ⊥BC于Q,过点A作AH⊥BC于H,连接OD,则CH= ![]() BC=6,由⊙O和线段DE相切,得出OG=
BC=6,由⊙O和线段DE相切,得出OG= ![]() AC=5,求出cosC=
AC=5,求出cosC= ![]() =
= ![]() ,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL证得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB=
,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL证得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB= ![]() =cosC=
=cosC= ![]() ,即可得出结果.
,即可得出结果.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市地铁9号线梅林段的一项绿化工程由甲、乙两工程队承担,已知乙工程队单独完成这项工程所需的天数是甲工程队单独完成所需天数的
 ,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,平行四边形ABOC的对角线交于点M,双曲线y=
 (x<0)经过点B、M.若平行四边形ABOC的面积为12,则k= .
(x<0)经过点B、M.若平行四边形ABOC的面积为12,则k= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过学习,同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷.相信通过对下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
例:用简便方法计算:
 .
.解:

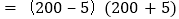 ①
①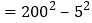 ②
②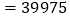 .
.(1)例题求解过程中,第②步变形是利用___________(填乘法公式的名称).
(2)用简便方法计算:
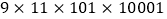 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.内错角相等,两直线平行).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
上述过程中判定依据错误的是( )
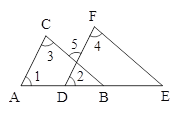
A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧
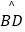 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC=  ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 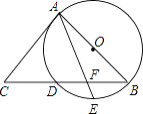
-
科目: 来源: 题型:
查看答案和解析>>【题目】将含30°角的三角板ABC如图放置,使其三个顶点分别落在三条平行直线上,其中∠ACB=90°,当∠1=60°时,图中等于30°的角的个数是()

A. 6个 B. 5个 C. 4个 D. 3个
相关试题

