【题目】如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料.
根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
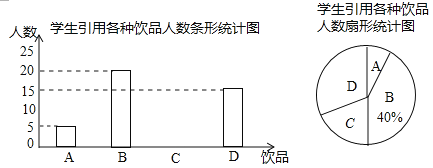
(1)这个班级有多少名同学?并补全条形统计图.
(2)若该班同学没人每天只饮用一种饮品(每种仅限1瓶,价格如下表),则该班同学用于饮品上的人均花费是多少元?

(3)若我市约有初中生4万人,估计我市初中生每天用于饮品上的花费是多少元?
(4)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,请用列表法或树状图法求出恰好抽到2名女生的概率.
参考答案:
【答案】(1)50;(2)2.6;(3)104000元;(4)![]() .
.
【解析】试题分析:(1)由B类型的人数及其百分比求得总人数,在用总人数减去其余各组人数得出C类型人数,即可补全条形图;
(2)由各类的人数可得其总消费,进而可求出该班同学用于饮品上的人均花费是多少元;
(3)用总人数乘以样本中的人均消费数额即可;
(4)用列表法或画树状图法列出所有等可能结果,从中确定恰好抽到一名男生和一名女生的结果数,根据概率公式求解可得.
试题解析:解:(1)∵抽查的总人数为:20÷40%=50人,∴C类人数=50﹣20﹣5﹣15=10人,补全条形统计图如下:

(2)该班同学用于饮品上的人均花费=(5×0+20×2+3×10+4×15)÷50=2.6元;
(3)我市初中生每天用于饮品上的花费=40000×2.6=104000元.
(4)列表得:

或画树状图得:
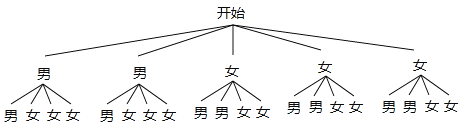
所有等可能的情况数有20种,其中一男一女的有12种,所以P(恰好抽到一男一女)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】-27的立方根与81的算术平方根的和是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,
△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
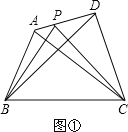
(1)当AP=
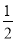 AD时(如图②):
AD时(如图②):∵AP=
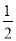 AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,∴S△ABP=
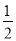 S△ABD.
S△ABD.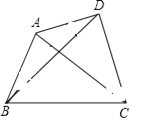
∵PD=AD﹣AP=
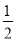 AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,∴S△CDP=
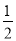 S△CDA.
S△CDA.∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣
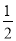 S△ABD﹣
S△ABD﹣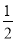 S△CDA
S△CDA=S四边形ABCD﹣
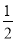 (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣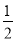 (S四边形ABCD﹣S△ABC)
(S四边形ABCD﹣S△ABC)=
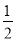 S△DBC+
S△DBC+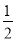 S△ABC.
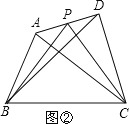
S△ABC.(2)当AP=
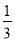 AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;(3)当AP=
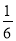 AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;(4)一般地,当AP=
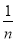 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;问题解决:当AP=
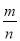 AD(0≤
AD(0≤ ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求
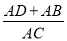 的值.
的值.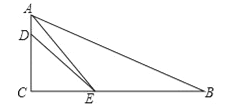
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠ACB=60°,∠ABC=50°,BO、CO分别平分∠ABC、∠ACB,EF是经过点O且平行于BC的直线,求∠BOC的度数。
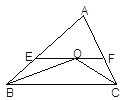
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
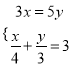 (2)
(2)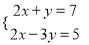
(3)
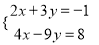 (4)
(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)ax4﹣ay4
(2)﹣4x2+12xy﹣9y2.
相关试题

