【题目】数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么![]() ,如何将双重二次根式
,如何将双重二次根式![]() 化简.我们可以把
化简.我们可以把![]() 转化为
转化为![]() 完全平方的形式,因此双重二次根式
完全平方的形式,因此双重二次根式![]() 得以化简.
得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若![]() 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
(1)点![]() 的“横负纵变点”为 ,点
的“横负纵变点”为 ,点![]() 的“横负纵变点”为 ;
的“横负纵变点”为 ;
(2)化简:![]() ;
;
(3)已知a为常数(1≤a≤2),点M(![]() ,m)是关于x的函数
,m)是关于x的函数![]() 图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)(﹣
;(3)(﹣![]() ,﹣
,﹣![]() )
)
【解析】
(1)根据“横负纵变点”的定义即可解决问题.
(2)模仿例题解决问题即可.
(3)首先化简双重二次根式,再根据待定系数法,“横负纵变点”解决问题即可.
解:(1)根据题目意思,![]()
∵![]() 和
和![]() ,
,
点![]() 的“横负纵变点”为
的“横负纵变点”为![]() ,点
,点![]() 的“横负纵变点”为
的“横负纵变点”为![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)∵![]()
∴![]() ;
;
(3)∵![]() ,
,![]()
![]()
∵点M(![]() ,m)是关于x的函数
,m)是关于x的函数![]() 图像上的一点,
图像上的一点,
∴![]() ,
,
即:M(![]() ,
,![]() ),
),
又∵点M’是点M的“横负纵变点
∴M′的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点在第一象限及
 轴、
轴、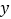 轴上运动,在第一秒钟,它从原点
轴上运动,在第一秒钟,它从原点 运动到
运动到 ,然后接着按图中箭头所示方向运动,即
,然后接着按图中箭头所示方向运动,即 →
→ →
→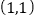 →
→ ,…,且每秒移动一个单位,到
,…,且每秒移动一个单位,到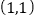 用时2秒,到
用时2秒,到 点用时6秒,到
点用时6秒,到 点用时12秒,…,那么到
点用时12秒,…,那么到 点用时________秒,第931秒时这个点所在位置坐标是_________.
点用时________秒,第931秒时这个点所在位置坐标是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点
 、
、 、
、 均在格点上.
均在格点上.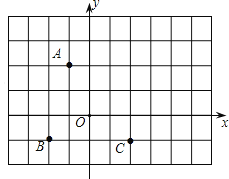
(1)请直接写出点
 、
、 、
、 的坐标分别为_________,_________,_________.
的坐标分别为_________,_________,_________.(2)若平移线段
 ,使
,使 移动到
移动到 的位置,请在图中画出
的位置,请在图中画出 移动后的位置
移动后的位置 ,依次连接
,依次连接 ,
, ,
, ,
, ,则四边形
,则四边形 的面积为________.
的面积为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DAE=∠E,∠B=∠D,试说明AB与DC平行.

解:因为∠DAE=∠E,(已知)
所以____∥____(_______)
所以∠D=____(_______)
因为∠B=∠D,(已知)
所以∠B=∠____(_______)
所以____∥____(_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.


①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A、B为反比例函数
 的图像上两点,A点的横坐标与B点的纵坐标均为1,将
的图像上两点,A点的横坐标与B点的纵坐标均为1,将 的图像绕原点O顺时针旋转90°,A点的对应点为A’,B点的对应点为B’.
的图像绕原点O顺时针旋转90°,A点的对应点为A’,B点的对应点为B’.(1)点A’的坐标是 ,点B’的坐标是 ;
(2)在x轴上取一点P,使得PA+PB的值最小,直接写出点P的坐标. 此时在反比例函数
 的图像上是否存在一点Q,使△A’B’Q的面积与△PAB的面积相等,若存在,求出点Q的横坐标;若不存在,请说明理由;
的图像上是否存在一点Q,使△A’B’Q的面积与△PAB的面积相等,若存在,求出点Q的横坐标;若不存在,请说明理由;(3)连接AB’,动点M从A点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动;动点N同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时,另一个点也随之停止运动.设运动的时间为t秒,试探究:是否存在使△MNB’为等腰直角三角形的t值.若存在,求出t的值;若不存在,说明理由.

相关试题

