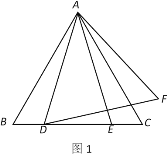
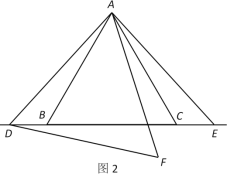
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:![]() .
.
参考答案:
【答案】(1)△ADF为等边三角形,见解析;(2)见解析
【解析】
(1)先根据等边三角形的性质得出![]() ,然后证明
,然后证明![]() ,得出
,得出![]() ,再根据对称的性质得出
,再根据对称的性质得出![]() ,从而有
,从而有![]() ,则结论可证;
,则结论可证;
(2)先根据等边三角形的性质得出![]() ,然后证明
,然后证明![]() ,得出
,得出![]() ,再根据对称的性质得出
,再根据对称的性质得出![]() ,从而有
,从而有![]() ,则△ADF为等边三角形,则
,则△ADF为等边三角形,则![]() ,通过等量代换即可得出答案.
,通过等量代换即可得出答案.
解:(1)△ADF为等边三角形,理由如下:
∵△ABC为等边三角形,
∴![]() .
.
在![]() 和
和![]() 中,
中,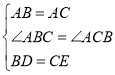
![]() ,
,
![]() .
.
∵点F,点E关于直线AC成轴对称,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
即![]() ,
,
∴△ADF为等边三角形.
(2)∵△ABC为等边三角形,
∴![]() .
.
在![]() 和
和![]() 中,
中,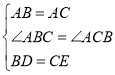
![]() ,
,
![]() .
.
∵点F,点E关于直线AC成轴对称,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴△ADF为等边三角形.
![]()
∵![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

-
科目: 来源: 题型:
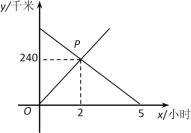
查看答案和解析>>【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足 时,y1>y2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y=
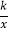 的图象有唯一的公共点C.
的图象有唯一的公共点C.(1)求k的值及C点坐标;
(2)直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y=
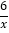 交于D、E两点,求△CDE的面积.
交于D、E两点,求△CDE的面积.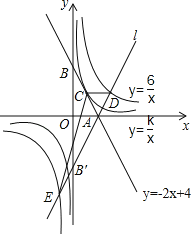
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)2x2-4x-10=0 (用配方法)
(2)2x2+3x=4(公式法)
(3)(x-2)2=2(x-2)
(4)
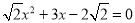
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
相关试题

