【题目】小明在上学的路上要经过多个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.
(1).如果有2个路口,求小明在上学路上到第二个路口时第一次遇到红灯的概率.(请用“画树状图”或“列表”等方法写出分析过程)
(2).如果有n个路口,则小明在每个路口都没有遇到红灯的概率是 .
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)画出树状图即可得到结果;
(2)先求出前几次都没有遇到红灯的概率,然后得到一般规律.
试题解析:解:(1)画树状图如下:
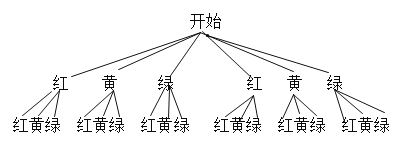
一共有18种情况,小明在上学路上到第二个路口时第一次遇到红灯有4种情况,∴P(在第二个路口第一次遇到红灯)=![]() ;
;
(2)P(第一个路口没有遇到红灯)=![]() ,P(前两个路口没有遇到红灯)=
,P(前两个路口没有遇到红灯)=![]() ,类似地可以得到P(每个路口都没有遇到红灯)=
,类似地可以得到P(每个路口都没有遇到红灯)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某条公共汽车线路收支差额
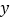 与乘客量
与乘客量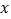 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额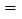 车票收入
车票收入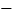 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )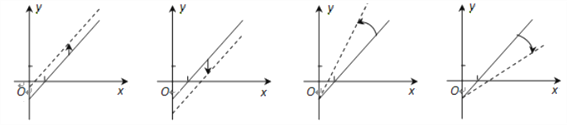
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
-
科目: 来源: 题型:
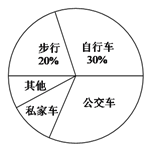
查看答案和解析>>【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC为等腰三角形,AB=AC
(1) 作BD⊥AC于D,若CD=2,BD=4,求AB的长度
(2) 若AB=2,E为BC延长线上一点,且AE=4.若BC∶CE=2∶3,判断△ABE的形状,并证明结论


-
科目: 来源: 题型:
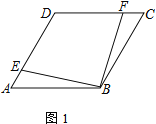
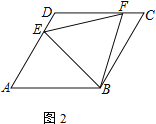
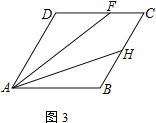
查看答案和解析>>【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】股民李明上星期六买进春兰公司股票1000股,每股27元.下表为本周内每日该股票的涨跌情况(单位:元)(注:本周一股票涨跌是在上周六的基础上,用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期
一
二
三
四
五
六
每股涨跌
+4
+4.5
-1
-2.5
-6
+2
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)己知李明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果李明在星期六收盘前将全部股票卖出,他的收益情况如何?
相关试题

