【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是( )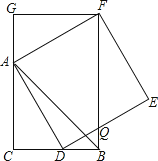
A.1
B.2
C.3
D.4
参考答案:
【答案】D
【解析】解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠C=90°=∠ACB,
∴∠CAD=∠AFG,
在△FGA和△ACD中, 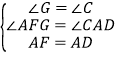 ,
,
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB= ![]() FBFG=
FBFG= ![]() S四边形CBFG , ②正确;
S四边形CBFG , ②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,④正确;
故选:D.
本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB= ![]() FBFG=
FBFG= ![]() S四边形CEFG , ②正确;
S四边形CEFG , ②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出DFE=AD2=FQAC,④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
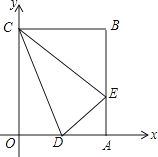
A.(3,1)
B.(3, )
)
C.(3, )
)
D.(3,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=
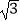 ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )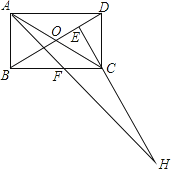
A.②③
B.③④
C.①②④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE=
 ,则另一直角边AE的长为( ).
,则另一直角边AE的长为( ).
A.
B.2
C.8
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D , 交AB于点E , 且BE=BF , 添加一个条件,仍不能证明四边形BECF为正方形的是( ).
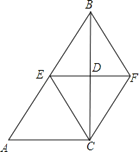
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
相关试题

