【题目】如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ![]() ,则另一直角边AE的长为( ).
,则另一直角边AE的长为( ).
A.![]()
B.2
C.8
D.10
参考答案:
【答案】D
【解析】过点O作OM⊥AE于点M , 作ON⊥DE , 交ED的延长线于点N , ∵∠AED=90°,∴四边形EMON是矩形,∵正方形ABCD的对角线交于点O , ∴∠AOD=90°,OA=OD , ∴∠AOD+∠AED=180°,∴点A , O , D , E共圆,∴∠AEO=∠DEO= ![]() ∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE=
∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE= ![]() ,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中
,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中 ![]() ,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.
,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.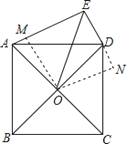
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论: ① 的值不变,②
的值不变,②  的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.

-
科目: 来源: 题型:
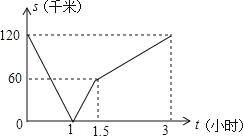
查看答案和解析>>【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,∠A=35°30′,则∠B=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的解析式是( ).

A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
相关试题

