【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是_____;
(2)补全频数分布直方图,并求扇形图中“15吨~20吨”部分的圆心角度数;
(3)用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
参考答案:
【答案】(1)100;(2)图详见解析,72°;(3)3.96万.
【解析】
(1)用10吨~15吨的用户除以所占的百分比,计算即可得解;(2)用总户数减去其它四组的户数,计算求出15吨~20吨的用户数,然后补全直方图即可;用“15吨~20吨”所占的百分比乘以360°计算即可得解;(3)用享受基本价格的用户数所占的百分比乘以6万,计算即可.
(1)10÷10%=100;
(2)用水量在15-20吨之间的用户数量:100-(10+36+25+9)=100-80=20
补全频数分布直方图如图:

扇形图中“15吨~20吨”部分的圆心角的度数: ![]()
(3)样本中少于25吨的有10+20+36=66(户)
∴少于25吨的户数是: ![]() (万户)
(万户)
∴该地区6万用户中约3.96万用户的用水全部享受基本价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展科技创新活动,在一次用电脑程序控制小型赛车进行50m比赛的活动中,“梦想号”和“创新号”两辆赛车在比赛前进行结对练习,两辆车从起点同时出发,“梦想号”到达终点时,“创新号”离终点还差2m.已知“梦想号”的平均速度比“创新号”的平均速度快0.1m/s.
(1)求“创新号”的平均速度;
(2)如果两车重新开始练习,“梦想号”从起点向后退2m,两车同时出发,两车能否同时到达终点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+
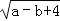 =0.
=0.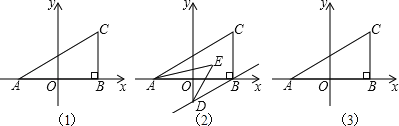
(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①近似数0.010精确到千分位;②如果两个角互补,那么两个角一定是一个为锐角,另一个为钝角;③若线段AP=BP,则P一定是AB中点;④A与B两点间的距离是指连接A、B两点间的线段;⑤│
 │=
│=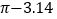 ;⑥最大的负整数是-1,其中说法正确的是_________.(填序号)
;⑥最大的负整数是-1,其中说法正确的是_________.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1,3,5,7,9,……,排成如图所示的数阵.
(1)十字框中五个数的和与中间数15有什么关系?
(2)设中间数为a,用式子表示十字框中五个数的和;
(3)若将十字框上下左右移动,可框住另外五个数,这五个数的和还有种规律吗?
(4)十字框中五个数之和能等于2010吗?若能,请写出这五个数;若不能,请说明理由.

相关试题

