【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+![]() =0.
=0.
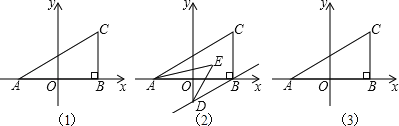
(1)求三角形ABC的面积.
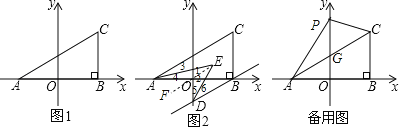
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)4;(2)45°;(3)P点坐标为(0,3)或(0,﹣1).
【解析】
试题分析:(1)根据非负数的性质得到a=﹣b,a﹣b+4=0,解得a=﹣2,b=2,则A(﹣2,0),B(2,0),C(2,2),即可计算出三角形ABC的面积=4;
(2)由于CB∥y轴,BD∥AC,则∠CAB=∠ABD,即∠3+∠4+∠5+∠6=90°,过E作EF∥AC,则BD∥AC∥EF,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)先根据待定系数法确定直线AC的解析式为y=![]() x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
解:(1)∵(a+b)2≥0,![]() ≥0,
≥0,
∴a=﹣b,a﹣b+4=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2)
∴三角形ABC的面积=![]() ×4×2=4;
×4×2=4;
(2)∵CB∥y轴,BD∥AC,
∴∠CAB=∠ABD,
∴∠3+∠4+∠5+∠6=90°,
过E作EF∥AC,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠4=∠1,∠5=∠6=∠2,
∴∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)存在.理由如下:
设P点坐标为(0,t),直线AC的解析式为y=kx+b,
把A(﹣2,0)、C(2,2)代入得![]() ,
,
解得![]() ,
,
∴直线AC的解析式为y=![]() x+1,
x+1,
∴G点坐标为(0,1),
∴S△PAC=S△APG+S△CPG=![]() |t﹣1|2+
|t﹣1|2+![]() |t﹣1|2=4,解得t=3或﹣1,
|t﹣1|2=4,解得t=3或﹣1,
∴P点坐标为(0,3)或(0,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣3+(﹣5)的结果是( )
A.﹣2
B.﹣8
C.8
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动﹣旋转变换
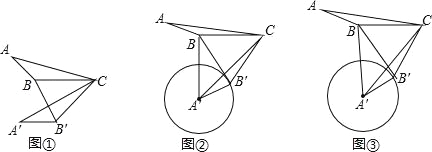
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同一种规格的下列多边形瓷砖不能镶嵌成平面图案的是( )
A.三角形B.正方形C.正五边形D.正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:

(2) 解方程组

(3)解方程组

(4)如果关于x,y的方程组
 的解满足3x+y=5,求k的值
的解满足3x+y=5,求k的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求
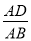 的值;
的值;(3)类比探求:
保持(1)中条件不变,若DC=nDF,求
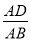 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一些分别标有-1,2,-4,8,-16,32,…的卡片,这些卡片上的数字是按一定规律排列的,小明拿到了相邻的三张卡片,且卡片上的数字之和为96,则小明拿到的三张卡片上分别标有什么数字?
相关试题

