【题目】将连续的奇数1,3,5,7,9,……,排成如图所示的数阵.
(1)十字框中五个数的和与中间数15有什么关系?
(2)设中间数为a,用式子表示十字框中五个数的和;
(3)若将十字框上下左右移动,可框住另外五个数,这五个数的和还有种规律吗?
(4)十字框中五个数之和能等于2010吗?若能,请写出这五个数;若不能,请说明理由.

参考答案:
【答案】(1) 5倍;(2) 5a;(3) 见解析;(4)见解析.
【解析】
(1)先求出这5个数的和,用这个和去除以中间的这个数15就可以得出结论;(2)设中间数为a,由左右相邻两个奇数之间相差2,上下相邻两个奇数之间相差10,就可以分别表示出这5个数,进而得出结论;(3)同样设中间数为b,就可以表示出这5个数的和,得出结论与(1)一样;(4)设中间的一个数为x,建立方程求出x的值就可以得出结论.
解:(1)由题意,得5+13+15+17+25=75.
75÷15=5.
∴十字框中的五个数的和是中间数15的5倍;
(2)设中间数为a,则其余的4个数分别为a-2,a+2,a-10,a+10,
由题意,得:![]() .
.
答:5个数之和为5a;
(3)设中间数为b,则其余的4个数分别为b-2,b+2,b-10,b+10,
由题意,得:![]() .
.
∴这五个数的和还是中间这个数的5倍;
(4)设中间数为x,则其余的4个数分别为x-2,x+2,x-10,
由(2)可知:5x=2010 解得:x=402.
∵402为偶数,
∴不存在十字框中五数之和等于2010.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是_____;
(2)补全频数分布直方图,并求扇形图中“15吨~20吨”部分的圆心角度数;
(3)用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+
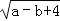 =0.
=0.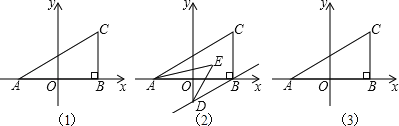
(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①近似数0.010精确到千分位;②如果两个角互补,那么两个角一定是一个为锐角,另一个为钝角;③若线段AP=BP,则P一定是AB中点;④A与B两点间的距离是指连接A、B两点间的线段;⑤│
 │=
│=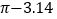 ;⑥最大的负整数是-1,其中说法正确的是_________.(填序号)
;⑥最大的负整数是-1,其中说法正确的是_________.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.纸上有5个边长为1的小正方形组成的纸片,可把它剪拼成一个正方形(图2)
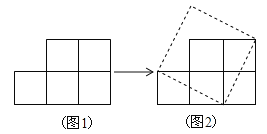
 (图3)
(图3)拼成的正方体的面积与边长分别是多少?
你能把这十个小正方体组成的图形纸(图3),剪拼成一个大正方形吗?若能,则请画出剪拼成的大正方形,并求出其边长为多少?
相关试题

