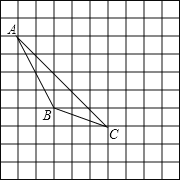
【题目】如图,每个小正方形的边长均为1,每个小方格的顶点叫格点
(1)画出△ABC中AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是:______;
(4)S△ABC的面积是______.
参考答案:
【答案】(1)见解析;(2)见解析;(3)平行且相等;(4)5
【解析】
(1)根据三角形中线的概念求解可得;
(2)将三个顶点分别向右平移4个单位得到对应点,再顺次连接即可得;
(3)由平移的性质可得;
(4)利用割补法求解可得.
解:(1)如图所示,CD即为所求;

(2)如图所示,△A1B1C1即为所求;
(3)由平移性质知AC与A1C1的关系是平行且相等,
故答案为:平行且相等;
(4)S△ABC的面积是![]()
故答案为:5.
-
科目: 来源: 题型:
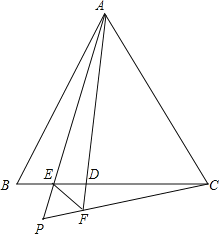
查看答案和解析>>【题目】如图,在△ABC中,点D为线段BC上一点(不含端点),AP平分∠BAD交BC于E,PC与AD的延长线交于点F,连接EF,且∠PEF=∠AED.
(1)求证:AB=AF;
(2)若△ABC是等边三角形.
①求∠APC的大小;
②想线AP,PF,PC之间满足怎样的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
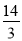 C.3D.
C.3D.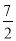
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有两个不相等的实数根?
(3)若x1,x2是方程的两个实数根,且xx2+x1x=-
 ,试求实数m的值.
,试求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
(1)求证:CE=CF;
(2)若点G在AD边上,且∠GCE=45°,BE=3,DG=5,求GE的长.
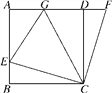
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ABC中,∠BAC=60°,内角∠ABC、∠ACB的平分线相交于点O,则∠BOC=______;
(2)如图2,△ABC中,∠BAC=60°,AD是△ABC的边BC上的高,且∠B=∠1,求∠C的度数.
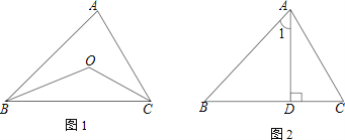
相关试题

