【题目】为推进阳光体育活动的开展,某学校决定开设以下体育课外活动项目:A 排球;B 乒乓球;C 篮球;D 羽毛球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图补充完整;
(3)求喜欢排球人数所占扇形圆心角的大小;
(4)若甲、乙、丙、丁四位同学都喜欢乒乓球运动,现从这四名同学中任选两名进行对抗练习, 求恰好选中乙、丙两位同学的概率(用树状图或列表法解答).
参考答案:
【答案】
(1)解:根据题意得:这次被调查的学生共有40÷ ![]() =200(人),故答案为:200;
=200(人),故答案为:200;
(2)解:C项目对应人数为:200-20-80-40=60(人),补充如图:

(3)解:喜欢排球人数所占扇形圆心角的大小为: ![]() ×360°=36°;
×360°=36°;
(4)解:列表如下
甲 | 乙 | 丙 | 丁 | |
甲 |  ̄ ̄ | (乙,甲) | (丙,甲) | (丁,甲) |
乙 | (甲,乙) |  ̄ ̄ | (丙,乙) | (丁,乙) |
丙 | (甲,丙) | (乙,丙) |  ̄ ̄ | (丁,丙) |
丁 | (甲,丁) | (乙,丁) | (丙,丁) |  ̄ ̄ |
∵共有12种等可能的情况,恰好选中乙、丙两位同学的有2种,
∴P(选中乙、丙)= ![]() =
= ![]() .
.
【解析】(1)先根据D的圆心角的度数求出D所占的百分比,然后用D的人数除以D所占的百分比,即可求出这次被调查的学生的人数。
(2)求出C项目对应人数,即可补全条形统计图。
(3)要求喜欢排球人数所占扇形圆心角,先求出喜欢排球人数所占的百分比,然后求出圆心角的度数。
(4)先列表或树状图,求出所有的等可能结果数及恰好选中乙、丙两位同学的可能数,利用概率公式即可求解。
【考点精析】掌握全面调查与抽样调查和扇形统计图是解答本题的根本,需要知道全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查;抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度;能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于
 的方程
的方程  没有实数根,则二次函数
没有实数根,则二次函数 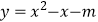 的图象的顶点在第象限.
的图象的顶点在第象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小刚从点
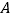 出发,沿着坡度为
出发,沿着坡度为 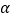 的斜坡向上走了650米到达点
的斜坡向上走了650米到达点 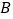 ,且
,且 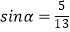 .
.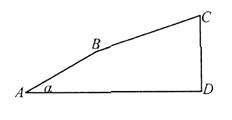
(1)则他上升的高度是 米 ;
(2)然后又沿着坡度为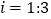 的斜坡向上走了1000米达到点
的斜坡向上走了1000米达到点 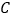 .问小刚从
.问小刚从 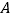 点到
点到 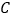 点上升的高度
点上升的高度 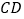 是多少米(结果保留根号)?
是多少米(结果保留根号)? -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组),并把解集在数轴上表示出来.
(1)

(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的网格中的每个小正方形边长都是1,线段交点称作格点.任意连接这些格点,可得到一些线段.按要求作图:
(1)请画出△ABC的高AD;
(2)请连接格点,用一条线段将图中△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积是_____________.

相关试题

