【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
参考答案:
【答案】(1) 北偏东70°;(2) ∠AOE=90°
【解析】
(1)先求出![]() ,再求得
,再求得![]() 的度数,即可确定
的度数,即可确定![]() 的方向;
的方向;
(2)根据![]() ,
,![]() ,得出
,得出![]() ,进而求出
,进而求出![]() 的度数,根据射线
的度数,根据射线![]() 平分
平分![]() ,即可求出
,即可求出![]() 再利用
再利用![]() 求出答案即可.
求出答案即可.
解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与直线
 相离,圆心
相离,圆心 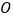 到直线
到直线  的距离
的距离  ,
,  ,将直线
,将直线  绕点
绕点  逆时针旋转
逆时针旋转  后得到的直线
后得到的直线  刚好与⊙O相切于点
刚好与⊙O相切于点  ,则⊙O的半径= .
,则⊙O的半径= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线AB∥射线CD,P为一动点,AE平分∠PAB,CE平分∠PCD,且AE与CE相交于点E.

(1)在图1中,当点P运动到线段AC上时,∠APC=180°.
①直接写出∠AEC的度数;②求证:∠AEC=∠EAB+∠ECD;
(2)当点P运动到图2的位置时,猜想∠AEC与∠APC之间的关系,并加以说明;
(3)当点P运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由;若不成立,请写出∠AEC与∠APC之间的关系,并加以证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于
 的方程
的方程  没有实数根,则二次函数
没有实数根,则二次函数 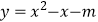 的图象的顶点在第象限.
的图象的顶点在第象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进阳光体育活动的开展,某学校决定开设以下体育课外活动项目:A 排球;B 乒乓球;C 篮球;D 羽毛球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的学生共有 人;
(2)请你将条形统计图补充完整;
(3)求喜欢排球人数所占扇形圆心角的大小;
(4)若甲、乙、丙、丁四位同学都喜欢乒乓球运动,现从这四名同学中任选两名进行对抗练习, 求恰好选中乙、丙两位同学的概率(用树状图或列表法解答).
相关试题

